КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ ДЕМОГРАФИЧЕСКИХ ПРОЦЕССОВ

Аннотация
В статье описаны возможности применения методов компьютерного моделирования в области социологии. Обсуждаются вопросы прогнозирования динамики популяции. Приведены некоторые математические модели, которые используются при исследовании демографических процессов.

Ключевые слова: демография, компьютерная модель, компьютерное моделирование в социологии, популяционная динамика., социальные процессы

Общество – это сложная динамическая система, в которой существуют проблемы актуальные не одно столетие. Поведение человека, социальной группы, общества порой кажется необъяснимым и непредсказуемым. Однако, ученые социологи, психологи и философы считают, что общественные явления подчиняются определенным закономерностям, которые могут быть описаны на языке математики. Компьютерное моделирование в области социологии является инструментом мониторинга и прогнозирования демографической ситуации в стране и может активно использоваться для корректировки правительственного курса и стабилизации прироста населения в России.

Выделим социальные проблемы, которые являются общими для многих стран мира: социальное неравенство, бедность, терроризм, преступность, коррупция. В России сегодня особенно актуальны низкий уровень жизни, алкоголизация населения, наркомания, безработица, высокая смертность. Все перечисленные тенденции негативно влияют на демографическую ситуацию в стране. На 1 января 2017 года население России составляло чуть меньше 150 миллионов человек. Невысокая численность населения в России связана с обширными территориями государства, потерями населения во время второй мировой войны, а также с последствиями провальной экономической политики правительства 90-х годов. Наш президент В.В. Путин оценил демографическую ситуацию в стране лаконичной фразой: «Либо мы будем, либо нас не будет». Авторитетный российский демограф, доктор философских наук А. Антонов пишет: «Хотя в последние пять лет рождаемость действительно несколько увеличилась, до 1,5-1,6 ребенка на женщину. Но нам нужно не меньше 2,2 чтобы население не уменьшалось, ни увеличивалось. При сохранении нынешнего уровня через 50 лет в России будет не 144, а 72 миллиона жителей». Объясняется подобная статистика достаточно просто: страна испытывает колоссальные экономические трудности, что, отражается на наличии рабочих мест и уровне жизни населения.

В нашей стране проблемы с демографией начались со времён кризиса 1990-ых годах, когда резко сократилась рождаемость и выросла смертность. В 1991 г. по численности населения Россия занимала шестое место в мире, в 2012 г. – десятое место, к 2050 г. Россия может оказаться на четырнадцатом месте. Демографическая ситуация несколько стабилизировалась в РФ только к 2013 году такими мерами правительства как материнский капитал, поддержкой многодетных семей, социальными пособиями, но динамика изменения естественного прироста демонстрирует превышение рождаемости над смертностью только в нескольких федеральных округах России, а значит проблема остаётся актуальной.

Исследовать, делать прогнозы, заниматься мониторингом динамики численности населения помогает компьютерное моделирование. Компьютерное моделирование в социологии – это метод исследования социальных явлений и процессов, опосредованное изучение социальных групп, в результате чего они воспроизводятся на компьютерной модели, заменяющей оригинал и позволяющей получать новые знания о предмете исследования.

Над проблемой демографических явлений работают многие учёные, как отечественные, так и зарубежные. К зарубежным учёным, которые внесли существенный вклад по изучению этого вопроса можно отнести: Д. Граунта, У. Петти, Э. Галлея, Л. Кетле, Ж. Бертильона, Г. Кинга, Т. Мальтуса, Ферхюльста, Д. Форрестера, Д. Медоуза, У. Фарра, А.Д. Лотки, В. Лексиса, М. Кремера, П.К. Уэлптона и др. В нашей стране первый прогноз динамики и структуры населения был выполнен еще в 1921 г. под руководством Е. Тарасова и С.Г. Струмилина. В его основу были положены итоги переписи населения 1920 г. Большой вклад в исследование демографических процессов внесли отечественные ученные: И.Ф. Герман, Д.К. Шелестов, В.И. Покровский, В.И. Гребенщиков, А.Я. Боярский, С.П.Капица, А.В. Подлазов, А.В. Коротаев, А.С. Малков, Д.А. Халтурина, Д.И. Валентей, А.Я. Кваша, Д. Эдиев, В.А. Борисов и др. [16, с. 4]. Результаты научных исследований ориентированы на изучение и прогнозирование демографических процессов, как в отдельной стране, так и во всем мире. Они являются научно – методической основой для дальнейшего научного поиска.

Демографические модели воспроизводят динамику половой и возрастной структуры населения в странах или регионах. Внутренними характеристиками является количество женщин и мужчин в текущем году, имеющих возраст от 0 до 100 лет. Внешними параметрами модели является распределение населения страны по полу и возрасту в исходном году, т. е. в том году, с которого начинается модельное воспроизведение демографического процесса, а также зависимости коэффициентов рождаемости и смертности от возраста, образованности, экологических факторов, от состояния системы здравоохранения. Прогностическими характеристиками, кроме упомянутых выше, также являются: общая численность населения в стране, численность мужчин, численность женщин, количество родившихся и умерших в данном году, численность детей от 0-го года до 6 лет,  численность школьников,  численность студентов, численность аспирантов; численность рабочих (от 18 лет до 59 ─ мужчины и женщины, окончившие школу, но не получившие высшего образования); численность служащих (от 23 лет до 59 ─ мужчины и женщины с высшим образованием); численность ученых (возраст от 25 лет до 59 ─ мужчины и женщины, окончившие аспирантуру); численность активного населения, т. е. суммарная численность рабочих, служащих, ученых, численность пенсионеров; отношение численности пенсионеров к численности активного населения [1, с. 9 ].

В работах многих ученых, в том числе С. А. Тимофеева и Д.В Помазкина рассматриваются ряд демографических моделей, описывающих зависимость темпов роста популяции от ее численности в предыдущий период во времени:
  - модель экспоненциального роста;

 - модель гиперболического роста;

 - логистическое уравнение,

где, P – суммарная численность населения, - коэффициенты, зависящие от времени. В качестве граничных условий задается число новорожденных, определенное согласно функции рождаемости, зависящей от возраста матери и времени [13, с. 1].

Модель экспоненциального роста предполагает неограниченное увеличение численности популяции. В гиперболической модели темп роста численности популяции пропорционален квадрату численности населения. Очевидно, что эти модели не могут точно отражать реальное положение дел для человеческой популяции, поскольку существует множество факторов, ограничивающих этот рост: территория, экология, ресурсы и т.д. Если предположить, что темп роста популяции замедляется с ростом численности населения, получаем логистическое уравнение:

где x – возраст; s – пол; t – время; P(x,s,t) – численность населения;

 - вероятность смерти среди населения; Migr (x,s,t) – нетто миграция.

Более корректным представляется логистическое уравнение, поскольку при широком наборе параметров его решение ограничено, что интуитивно кажется правдоподобным. Допустим, что численность населения можно моделировать при помощи уравнения экспоненциального роста, предположив, что в некоторые моменты времени возникают резкие сокращения численности. Данное явление моделируется введением дополнительной функции, приводящей уравнение экспоненциального роста к следующему виду:

Решение данного уравнения, полученное при следующих параметрах (a=0.015, t=40, 80 ,….,k-линейная функция обращающаяся в ноль при максимальном t. K(0)=0,58. Начальная численность равна 0.5), представлено на рисунке 1. Если предположить, что размерность результатов, приведенных на рисунке 1 в млрд., то полученная зависимость является хорошим приближением динамики численности населения Земли [13, с. 2].

Рисунок 1 - Изменение численности населения Земли (млрд. чел.)

В государственной статистике используется демографические таблицы рождаемости и смертности, которые представляют собой систему взаимосвязанных упорядоченных по возрасту чисел. Эти числа описывают процессы роста населения в связи с рождаемостью и убыль населения в связи со смертностью теоретического поколения с фиксированной начальной численностью (в возрасте 15 лет для прироста и с 0 лет для смертности). Таблицы рождаемости и смертности рассчитываются для мужчин, женщин и двух полов суммарно [2]. Перспективные расчеты численности населения строятся на основе гипотез относительно будущей динамики рождаемости, смертности, миграции. Прогнозирование демографической динамики производится на основе численности населения, полученной как по данным переписи населения, так и по текущим оценкам таблиц рождаемости и смертности, текущей статистической отчетности.

Общий вид математической модели:

S(x+1,t+1) = S(x,t)´P(x,t) + W(x,t), где

• S(x+1,t+1) – численность населения через год в следующей возрастной группе;
• S(x,t) – численность населения в возрастной группе;
• P(x,t) – коэффициент дожития;
• W(x,t) – объем миграции, заложенный в расчет, распределенный по полу и возрасту.

Ожидаемое число родившихся в году t рассчитывается путем умножения численности женщин в возрасте 15 – 49 лет на соответствующие коэффициенты рождаемости, полученные из таблиц рождаемости:

N(t) = S(15,t) × F(15,t) + … + S(49,t) × F(49,t), где

• N(t) – число родившихся;
• F(х,t) – коэффициенты рождаемости, полученные из таблиц рождаемости;
• S – среднегодовая численность женщин.

Прогнозное число умерших в году t определяется как разность между численностью населения на начало года и численностью населения, передвинутая на конец года. Расчет умерших определяется по формуле:

M(t) = Σ(1 – P(x,t) × S(x,t) + N(t) × (1 – P(N,t)), где

• M(t) – число умерших;
• P(N,t) – коэффициент дожития новорожденных до конца года.

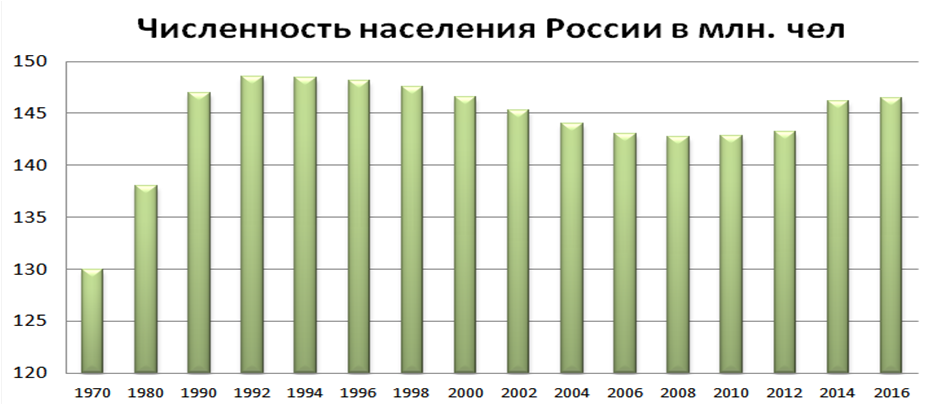
На основе математических моделей можно предсказывать изменение демографической ситуации в будущие периоды времени как для отдельных регионов и областей РФ, так и для страны в целом. Сравнивая прогнозные (рис. 3) и реальные показатели (рис. 2) за предыдущие периоды можно оценить влияние различных факторов на население [10]. Так линейная трендовая модель свидетельствует о том, что потери населения в России в 90-ые годы превышают 20 млн. человек.

Рисунок 2 – Распределение численности населения РФ с 1970 по 2016 годы

Рисунок 3 – Линейный прогноз численности населения РФ с 1970 по 2016 годы

Достоверность демографических прогнозов зависит от множества факторов. Научно обоснованные предположения о динамике репродуктивного, самосохранительного и миграционного поведения населения безусловно повышают надежность результатов компьютерного моделирования. Стоит отметить, что компьютерные демографические модели не обладают высокой точностью прогнозов, но результаты расчетов близки к действительной демографической ситуации и, опираясь на них можно предсказать тенденции развития общества. Компьютерное моделирование в социологии – это современный и эффективный метод, который предоставляет возможность производить мониторинг демографических процессов в реальном времени, исследовать и выявлять факторы, которые оказывают наибольшее влияние на стабилизацию демографического положения в стране, и, исходя из этого формировать эффективную социально-экономическую политику в государстве.

Библиографический список

1. Белотелов Н.В., Бродский Ю.И., Павловский Ю.Н. Компьютерное моделирование демографических, миграционных, эколого-экономических процессов средствами распределённых вычислений: научное издание. – Москва: изд-во Российская академия наук, вычислительный центр им. А.А Дородницына, 2008. – 123 с. – URL: http://simul.ccas.ru/articles/Monograf.pdf
2. Гусева Е.Н. Имитационное моделирование социально-экономических процессов. – Магнитогорск: изд-во Магнитогорск. гос. техн. ун-та им. Г.И. Носова, 2015. – 25с.
3. Гусева Е.Н. Имитационное моделирование экономических процессов в среде «Arena»: учеб. пособие: [электронный ресурс]. М.: Флинта, 2011. – 132 с. – URL: http://www.knigafund.ru/books/114189
4. Гусева Е.Н. Моделирование макроэкономических процессов: учеб. пособ.: [электронный ресурс]/ Е. Н. Гусева. – М.: Флинта, 2014. -214с.- Режим доступа: http://www.ozon.ru/context/detail/id/28975354/
5. Гусева Е.Н. Основы имитационного моделирования экономических процессов: лаб. практикум / Е.Н. Гусева. – Магнитогорск: МаГУ, 2008. – 100с.
6. Гусева Е.Н., Варфоломеева Т.Н. Применение имитационных моделей для решения экономических задач оптимизации/Гусева Е.Н., Т.Н. Варфоломеева //Современные проблемы науки и образования. 2014. № 6. С. 200.
7. Ермакова Т.А., Гусева Е.Н. Использование компьютерного моделирования в преподавании геометрии // Современные научные исследования и инновации. 2016. № 6 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2016/06/68886 (дата обращения: 24.06.2016).
8. Капица С.П. Гиперболический путь человечества через демографическую революцию к обществам знаний. – М.: Издательский Дом Тончу, 2009. – 125с.
9. Коротаев А.В., Малков А.С., Халтурина Д.А. Законы истории: Математическое моделирование развития мир-система. Демография, экономика, культура. Москва, URSS, 2007.
10. Сайт о странах, городах, статистике населения и пр. [Электронный ресурс].  URL: http://www.statdata.ru/russia
11. Татарникова В.В., Гусева Е.Н. Использование компьютерного моделирования в решении задач о системах массового обслуживания // Современные научные исследования и инновации. 2016. № 6 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2016/06/69373 (дата обращения: 10.11.2016).
12. Тимофеев C.А., Помазкин Д.В. Демографические модели [электронный ресурс]/ Д.В. Помазкин, C.А. Тимофеев – Режим доступа: http://www.infoarchives.ru/data/dm.pdf
13. Тимофеев C.А., Помазкин Д.В. К вопросу о существовании демографической константы [электронный ресурс]/ Д.В. Помазкин, C.А. Тимофеев – Режим доступа: http://www.infoarchives.ru/data/demog_const.pdf
14. Тимофеев C.А., Помазкин Д.В. Проблема 25 [электронный ресурс]/ Д.В. Помазкин, C.А. Тимофеев – Режим доступа: http://www.infoarchives.ru/data/Problem_25.pdf
15. Чечулин В.Л, Смыслов В.И. Модели социально – экономической ситуации в России 1990 – 2010 годов и сценарные прогнозы до 2100 года: монография. – Пермь: изд-во Пермский Государственный национальный исследовательский университет, 2013. – 194 с. – URL: http://www.psu.ru/files/docs/science/books/mono/Chechulin_Smyslov_modeli_2013.pdf
16. Чучкалова С.В. Моделирование демографических процессов в Кировской области: автореферат. – Пермь: изд-во Пермский Государственный университет, 2011. – 23 с. – URL: http://www.psu.ru/psu2/files/0504/Chuchkalova_05_07_11.pdf