Математика цветов. Цветовое счастье.

Загляни, почитай, посчитай !!!
https://delphinium.webasyst.net/shop/
Интернет-магазин "Любимый сад"

Математика и цвет
Принципы математики цвета.
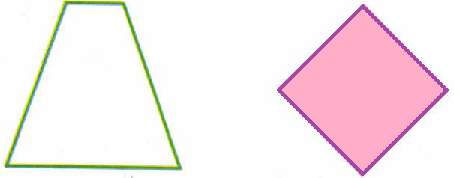
Принцип симметрии, утверждающий, что порядок, в котором цвета добавляются друг к другу, не изменяет результат (рис. 71).

Рис. 71. Принцип симметрии
Принцип совокупного объема. Добавление (или вычитание) из двух или более цветов, скорее всего, вызовет заметное изменение в оттенке, но особое внимание следует обратить на совокупный объем операции. Например, смешивание одной измеряемой единицы цвета с такой же приведет к увеличению объема полученного цвета в два раза (рис. 72).

Рис. 72. Принцип совокупного объема для одного цвета
Принцип совокупного объема относится и к операциям, связанным с различными цветами (рис. 73).

Рис. 73. Принцип совокупного объема для разных цветов
Сложение цветов.
Объединение голубого с пурпурным, голубого с желтым и пурпурного с желтым позволяет получить синий, зеленый и красный соответственно:
• 1 голубой (А) + 1 пурпурный (В) = 2 синий (АВ)

• 1 голубой (А) + 1 желтый (С) = 2 зеленый (АС)

• 1 пурпурный + 1 желтый = 2 красный

Эти операции справедливы при полном насыщении и эквивалентных количествах первичных ингредиентов.
Когда смешиваются все три основных цвета в равной пропорции, получается черный цвет:
1 голубой (А) + 1 пурпурный (В) + 1 желтый (Q = 3 черный (АВС)

Черный цвет также можно получить, если смешать определенные комбинации первичных и вторичных элементов, а именно: так как красный цвет состоит из равных частей пурпурного и желтого, то, смешав голубой с красным, получим черный:

ИЛИ
1 часть голубой (А) + 2 части красный (ВС) = 3 части черный (АВС)

Поскольку каждый вторичный цвет - это лишь сочетание двух первичных, черный является результатом в каждой из следующих смесей. Обратите внимание на неравные количества входов и постоянную величину суммы.


Рассмотрим случаи, когда вторичные цвета суммируются в равных количествах. Например, какой цвет получится при смешении красного, зеленого и синего:

Чтобы ответить на этот вопрос правильно, необходимо рассмотреть составные элементы этих цветов в цветовой модели CMY для исследования точного количества смешивания:

Анализ пропорций CMY в сумме показал, что результирующим цветом является черный:

Как было показано выше, каждый объем цвета стандартизирован до длины одного набора, поэтому можно сложить эти объемы вместе, чтобы определить конфигурацию их суммы.
Например, добавление к данному количеству 100 % базового белого цвета такого же количества 100 % первичного желтого даст цвет, который является наполовину основным, т. е. с 50 % желтого оттенка (рис. 74).
Это говорит о том, что, как только входные цвета сочетаются и смесь сбрасывается на стандартный размер (объем) первоначального цвета, результирующий цвет будет содержать равные части белого как базового цвета и желтого как основного.
Другая ситуация, когда к базовому белому цвету добавляется цвет, содержащий неравные количества нескольких основных цветов (рис. 75).

Рис. 74. Результат смешения двух однородных цветов

Рис. 75. Результат смешения двух неоднородных цветов
В данном примере складываются четыре части базового белого и четыре части первичных цвета, из которых три части пурпурного и одна часть желтого.
В результате два квадрата будут белыми, пурпурный и желтый займут 1,5 и 0,5 из оставшихся единиц соответственно.
На рис. 76 приведен пример смешивания трех цветов
Все ингредиенты собраны и сгруппированы по их категории CMYK. Калибровка всех цветовых сочетаний в фиксированной сумме важна, потому что этот процесс нормализации позволяет оценить цвета.
Возьмем для нашего следующего уравнения суммы двух последних операций и используем их в качестве вклада. После добавления цветных полос вместе, мы можем отсортировать и откалибровать сумму фиксированной суммы со всеми составляющими элементами нетронутыми (рис. 77).

Рис. 76. Результат смешения трех цветов

Рис. 77. Смешение многокомпонентных цветов
Таким образом, использование цветовых полос позволяет определить результирующий цвет на основе объективности процентных значений и количества цвета.







