Математический калейдоскоп
сайт для любознательных
Знания, получаемые школьниками на уроках во время изучения основного курса, не всегда являются достаточными. В связи с этим возрастает роль дополнительных занятий по математике, на которых можно углубить и систематизировать знания по основному курсу, получить дополнительную информацию, исходя из достижений математической науки.
Калейдоско́п (от греч. καλός — красивый, εἶδος — вид, σκοπέω — смотрю, наблюдаю) — оптический прибор-игрушка, чаще всего в виде трубки, содержащей внутри три (иногда два или более трёх) продольных, сложенных под углом зеркальных стекла; при поворачивании трубки вокруг продольной оси цветные элементы, находящиеся между зеркалами, отражаются и создают меняющиеся симметричные узоры. Различное взаимное расположение зеркал позволяет получить разное количество дублированных изображений: 45° — 8, 60° — 6, 90° — 4. В переносном смысле калейдоскоп - быстрая смена явлений, лиц, событий. Баснописец А.Измайлов писал:
Смотрю – и что же в моих глазах?
В фигурах разных и звездах
Сапфиры, яхонты, топазы,
И изумруды и алмазы,
И аметисты и жемчуг,
И перламутр – все вижу вдруг!
Лишь сделаю рукой движенье –
И новое в глазах явленье! Так и в математике. Одно движение - и новое явление!
Паначёва Ирина Евгеньевна
Службы по богачу
| Один богач оставил завещание, в котором написал, что завещает всё своё богатство тому монастырю, который отслужит по нему количество обеден, равное половине количества дней, оставшихся существовать этому монастырю. Много монастырей хотело получить это богатство, но не знало, как выполнить условие завещания. Наконец, настоятель одного монастыря сказал, что он знает, как выполнить условие завещания. Как же он собирался выполнить его? Обмен жидкостями Перед вами очень древняя задача:
|
Активные участники дистанционных конкурсов ЭМУ и Кенгуру, участники и призёры муниципального тура всероссийской олимпиады школьников
Вся информация о ЕГЭ и ГИА на сайте школы http://nsportal.ru/site/227794 в папке Выпускникам
http://eqworld.ipmnet.ru/ru/pastime/puzzles.htm -Развлечения > Занимательная математика: задачи, головоломки, игры.
Архив журнала «Квант» - http://www.kvant.info/old.htm.
http://www.zaba.ru/ -посвящена математическим олимпиадам - много отличных задач для любителей подумать! http://free-
math.ru/publ/zanimatelnaja_matematika/kunguru/57 -шесть сборников с решениями Международного конкурса-игры Кенгуру
Открытый архив олимпиады «Математический праздник» -http://olympiads.mccme.ru/matprazdnik/prob.html-
Математическая библиотека http://www.math.ru/
Сайт проблемс.ру -http://www.problems.ru/, где собраны свыше 20 тысяч задач для тех, кто ведет уроки, кружки и факультативные занятия.
Многоцелевой открытый банк заданий по ЕГЭ - http://opencollection.ru/.
Информационно-поисковая система «Задачи по геометрии», в этой базе 8 тысяч задач по геометрии с графическим решением. - http://zadachi.mccme.ru.
Занятия занимательной математики "Гимнастика ума" проводятся на последнем в четверти уроке математики.
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Курс дополнительных занятий рассчитан на учащихся 5-8 классов и включает в себя 20 аудиторных часа, по 5 часов в каждом из классов.
Основная цель данного курса: развитие творческих способностей школьников; формирование устойчивого интереса к математике.
Важной составной частью реформы общеобразовательной и профессиональной школы является повышение качества учебно-воспитательного процесса, в частности совершенствование математического образования.
Состояние математической подготовки учащихся характеризуется в первую очередь умением решать задачи. С другой стороны, задачи — это основное средство развития математического мышления учащихся. Очевидно, речь идет не об упражнениях тренировочного характера или задачах «на известный тип», а о нестандартных задачах, поиск решения которых, как и нестандартные решения традиционных задач, по словам академика Гнеденко Б. В., составляют важные слагаемые на пути развития способностей и духа творческого горения.
Не случайно в учебниках по математике нестандартным задачам отводится значительное место. Строишь ли ты скворечню, собираешь ли из деталей «Конструктора» техническую игрушку или вдумчиво выполняешь задание на уроке, участвуешь ли с ребятами в игре — всегда возникает необходимость что-то сосчитать, быстро сообразить, смекнуть, угадать. Не всегда сразу находится правильное решение. И ты можешь заметить, что тот быстрее сообразит, смекнет, угадает, кто чаще упражняется в решении задач,
головоломок, много мастерит, занимается отгадыванием различных хитроумных загадок.
Не только руки, ноги, тело, но и мозг человека требует постоянной тренировки, упражнений. В результате упражнений ум человека становится острее, а сам он — находчивее, сообразительнее.
Особенно полезны математические упражнения. «Недаром говорят, что математика—это гимнастика ума»,— утверждал М. И. Калинин.
С древнейших времен известно, что математика учит нас правильно и последовательно мыслить, логически рассуждать. Кто с детских лет занимается математикой, тот развивает свой ум и внимание, воспитывает волю и настойчивость. А эти качества нужны всем без исключения: и врачу, и артисту, и учителю, и художнику.
Для успешного освоения программы школьного обучения ребенку необходимо не только много знать, но и последовательно и доказательно мыслить, догадываться, проявлять умственное напряжение.. Интеллектуальная деятельность, основанная на активном поиске способов действийпри соответствующих условиях может стать привычной для детей.
Как известно, особую умственную активность ребенок проявляет в ходе достижения игровой цели как на занятии, так и в повседневной жизни. Игровые занимательные задачи содержатся в разного рода увлекательном математическом материале. В истории развития методики обучения детей математике накоплено довольно много подобного материала.
Слово «гимнастика»связано с представлением со спортивными упражнениями на брусьях, кольцах, перекладине, с красивыми, похожими на танец, движениями под музыку с обручем, мячом, лентами, с соревнованиями, которые часто показывают по телевизору.
Дополнительные математические занятия «Гимнастика для ума»специально направлены на развитие мышления учащихся. Курс занятий должен формировать логическую грамотность школьников и, наряду с этим, обеспечивать развитие (или, хотя бы неподавление) познавательного интереса и способностей, свойственных практически всем детям в школьном возрасте.
Развитие мышления — дело чрезвычайно тонкое, требующее тщательного соблюдения баланса между логикой и интуицией, словом и наглядным образом, осознанным и подсознательным.
Назначение дополнительного курса— способствовать формированию у младших школьников логической интуиции и элементов логической грамотности в единстве с развитием способности к непосредственному зрительному «схватыванию» объектов в их целостности, развитием подвижности и гибкости мышления, фантазии, воображения.
На занятиях учащиеся узнают много интересных задач, упражнений, игр, интересные факты из истории математики. Для занятий с ребятами собраны различные викторины, загадки, увлекательные рассказы...
Материал представлен в определенной системе, что важно для повышения уровня общего умственного развития ребят, подготовки их к усвоению курса математики в школе, для творческого труда в будущем. Занимательный математический материал, рассматривается и как одно из средств, обеспечивающих рациональную взаимосвязь работы учителя на занятиях и вне их.
Формы организации ребят разнообразны: игры проводятся со всеми учащимися, с группами и индивидуально. Педагогическое руководство состоит в создании условий для игр, поддержании и развитии интереса, поощрении самостоятельных поисков решений задач, стимулировании творческой инициативы.
Математические игры и головоломки очень популярны, как, впрочем, и все игры. И далеко не всегда более сложная игра - более интересная. Часто миллионы людей с неугасаемым интересом играют в самые простые игры, и именно эти игры больше всего ценят, именно они входят в историю математики и прославляют своих создателей.
Наиболее приближенными к математике являются головоломки, но много головоломок образовалось из когда-то существовавших (а некоторые из ещё существующих) игр. Большинство таких основополагающих игр было придумано древнегреческими математиками. Головоломки целесообразны при закреплении представлений ребят о геометрических фигурах, их преобразовании. Загадки, задачи-шутки уместны в ходе обучения решению арифметических задач, действий над числами, формирование временных представлений и т. д.
Смекалки, головоломки, занимательные игры вызывают у ребят большой интерес.
Ребята могут, не отвлекаясь, подолгу упражняться в преобразовании фигур, перекладывая палочки или другие предметы по заданному образцу, по собственному замыслу, В таких занятиях формируются важные качества личности ребенка: самостоятельность, наблюдательность, находчивость, сообразительность, вырабатывается усидчивость, развиваются конструктивные умения.Любая математическая задача на смекалку несет всебе определенную умственную нагрузку, которая чаще всего замаскирована занимательным сюжетом, внешними данными, условием задачи и т. д. В ходе решения задач на смекалку, головоломок дети учатся планировать свои действия, обдумывать их, догадываться в поисках результата, проявляя при этом творчество. Эта работа активизирует не только мыслительную деятельность школьника, но развивает у него качества, необходимые для профессионального мастерства, в какой бы сфере потом он ни трудился.
В самом начале занятий оправдывает себя использование несложных занимательных задач в качестве «умственной гимнастики». Занимательность математическому материалу придают игровые элементы, содержащиеся в каждой задаче, логическом упражнении, развлечении, будь то шахматы или самая элементарная головоломка.Занятия гимнастикой помогают стать сильным, ловким, гибким, стройным, храбрым, выносливым.
Гимнастика для ума— это упражнения для ума, тренировка ума, с помощью, которой ребенок научится четко и ясно мыслить, решать задачи и головоломки, разгадывая, загадки, шарады, ребусы, рассуждать, спорить, доказывать.
Тренируя ум, человек становится наблюдательным, сообразительным, проницательным, догадливым, дальновидным, изобретательным, находчивым, остроумным, а также приобретает многие другие важные и полезные качества, которые все вместе составляют культуру мышления или умственную культуру, так же, как сила, ловкость, выносливость и многое другое составляют физическую культуру.
ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА
1. Я. И. Перельман "Занимательная математика"
2. М. Гарднер "Путешествие во времени". - Москва, "Мир", 1990
3. В. Н. Дубровский, А. Т. Калинин "Математические головоломки". - Москва, "Знание", 1990
4. Игнатьев Е.И. В царстве смекалки. — М., 1978.
5. Илларионова Ю.Г. Учите детей отгадывать загадки. — 198
6. Козлова Е.Г. Сказки и подсказки. — М., 1994.
7. Компанией, В.Г. Игры и развлечения. — М., 1953.
8. Лэнгдон Н., Снэйп Ч. С математикой в пути. — М., 1987,
9. Минска» Е.М. От игры — к знаниям. — М., 1987.
10. Никольская И.Л„ Семенов Е.Е, Учимся рассуждать и доказывать. — М., 1989.
11. Русанов В.Н. Математические олимпиады младших школьников. — М., 1990.
12. Шарыгин И.Ф., Шевкин А.В. Подумай и реши. Задачи на смекалку. — М., 1993.
13. Детская периодическая печать.
ТЕМАТИЧЕСКИЙ ПЛАН ЗАНЯТИЙ
«ГИМНАСТИКА ДЛЯ УМА»
5 класс
№ п.п. | Цель | Содержание | Тема занятия | Приложения |
1
| Формирование интереса к изучению предмета, посредством знакомства с его историей. | Знакомство с историей математики. | Как научились люди считать и записывать числа.
| Приложение к журналу «Праздник числа». |
2 | Формирование простейших эвристических (поисковых) умений. | Поиск и выявление закономерностей. перекодирование информации: коды и шифры, графы, действия по алгоритму. комбинаторные задачи.
| ЗАДАЧИ НА ПЕРЕЛИВАНИЕ. Способы решения. | Подборка задач с решениями. |
3 | Формирование первоначальных логических представлений и умений, логической интуиции. | Простейшие умозаключения, рассуждения, доказательства на уровне интуитивно понимаемых правил логических выводов.
| ЛОГИЧЕСКИЕ ЗАДАЧИ Способы решения логических задач. | Подборка логических задач с решениями. |
4 | Формирование элементов творческого мышления, развитие наблюдательности, воображения, сообразительности. | Загадки, шарады, ребусы, кроссворды, метаграммы...
Игры «в слова». Игры и головоломки со спичками, геометрическими фигурами. | ЗАНИМАТЕЛЬНЫЕ КВАДРАТЫ. Правила заполнения.
| Мультимедийная презентация. |
РЕБУСЫ. Правила разгадывания ребусов. | Мультимедийная презентация. |
6 класс
№ п.п. | Цель | Содержание | Тема занятия | Приложения |
1
| Формирование интереса к изучению предмета, посредством знакомства с его историей. | Знакомство с историей математики. | Старинные меры в истории и речи народной.
| Приложение к журналу «Праздник числа». |
2 | Формирование первоначальных логических представлений и умений, логической интуиции. | Поиск и выявление закономерностей. перекодирование информации: коды и шифры, графы, действия по алгоритму. Комбинаторные задачи.
| ПЕРЕСТАНОВКИ и РАЗМЕЩЕНИЯ. | Подборка задач с решениями. |
3 | Формирование простейших эвристических (поисковых) умений. | Простейшие умозаключения, рассуждения, доказательства на уровне интуитивно понимаемых правил логических выводов.
| ЛОГИЧЕСКИЕ ЗАДАЧИ Способы решения логических задач. | Подборка логических задач с решениями. |
4 | Формирование элементов творческого мышления, развитие наблюдательности, воображения, сообразительности. | Загадки, шарады, ребусы, кроссворды, метаграммы...
Игры «в слова». Игры и головоломки со спичками, геометрическими фигурами. | ШАРАДЫ. Правила решения шарад.
| Мультимедийная презентация. |
КРОССВОРДЫ. Правила составления кроссвордов.
| Мультимедийная презентация. |
7 класс
№ п.п. | Цель | Содержание | Тема занятия | Приложения |
1
| Знакомство с занимательной литературой по математике. | Приобщение к миру занимательной литературы, формирование навыков планирования и проведения досуга. | И.Г.Сухин "Весёлая математика: 1500 головоломок для математических олимпиад, уроков, досуга: 5-7 класс" (М.: ТЦ "Сфера", 2003..) | Мультимедийная презентация. |
2 | Формирование простейших эвристических (поисковых) умений. | Поиск и выявление закономерностей, перекодирование информации: коды и шифры, графы, действия по алгоритму. Комбинаторные задачи.
| КОМБИНАТОРНЫЕ ЗАДАЧИ. Способы решения комбинаторных задач | Подборка комбинаторных задач с решениями. |
3
| Формирование первоначальных логических представлений и умений, логической интуиции. | Простейшие умозаключения, рассуждения, доказательства на уровне интуитивно понимаемых правил логических выводов.
| ЛОГИЧЕСКИЕ ЗАДАЧИ Способы решения логических задач. | Подборка логических задач с решениями. |
4 | Формирование элементов творческого мышления, развитие наблюдательности, воображения, сообразительности. | Загадки, шарады, ребусы, кроссворды, метаграммы...
Игры «в слова». Игры и головоломки со спичками, геометрическими фигурами. | МЕТАГРАММЫ. Правила решения метаграмм.
| Мультимедийная презентация. |
ЛОГОГРИФЫ. Правила решения логогрифов.
| Мультимедийная презентация. |
8 класс
№ п.п. | Цель | Содержание | Тема занятия | Приложения |
1
| Знакомство с занимательной литературой по математике. | Приобщение к миру занимательной литературы, формирование навыков планирования и проведения досуга. | И.Г.Сухин. "800 новых логических и математических головоломок" (СПб: Союз, 2001) | Мультимедийная презентация.
|
2 | Формирование простейших эвристических (поисковых) умений. | Поиск и выявление закономерностей. перекодирование информации: коды и шифры, графы, действия по алгоритму. комбинаторные задачи.
| КОМБИНАТОРНЫЕ ЗАДАЧИ. Способы решения комбинаторных задач | Подборка комбинаторных задач с решениями. |
3
| Формирование первоначальных логических представлений и умений, логической интуиции. | Простейшие умозаключения, рассуждения, доказательства на уровне интуитивно понимаемых правил логических выводов.
| ЛОГИЧЕСКИЕ ЗАДАЧИ Способы решения логических задач. | Подборка логических задач с решениями. |
4 | Формирование элементов творческого мышления, развитие наблюдательности, воображения, сообразительности. | Загадки, шарады, ребусы, кроссворды, метаграммы...
Игры «в слова». Игры и головоломки со спичками, геометрическими фигурами.
| СУДОКУ. Японская головоломка.
| Мультимедийная презентация. |
МИНИ-КАРАКУРО. Японская головоломка. | Мультимедийная презентация. |
В кабинете функционирует сменный стенд "Это интересно"
В кабинетной библиотеке собраны книги о занимательной математике.
Раз в два года проводится общешкольная математическая декада.
Книги Я.И. Перельмана: Занимательная арифметика, 1926 (книга - djvu) Занимательная математика, 1927 (книга - djvu) Живая математика, 1967 (книга - djvu) Занимательная алгебра, 1967 (книга - djvu) Занимательная геометрия, 1950 (книга - djvu) Занимательная механика, 1937 (книга - djvu) Занимательная физика, 1933 (книга - djvu) Занимательная астрономия, 1954 (книга - djvu) Занимательные задачи и опыты, 1959 (книга - djvu) Сайты и веб-страницы: Арбуз, замечательный сайт Е. Скляревского (Арбузные ломтики: математические картинки, юмор, задачки, стихи, парадоксы, иллюзии и др. Ссылки: лучшие страницы Рунета для любителей занимательной математики) Головоломки для умных людей, головоломки по разделам на любой вкус, статьи Гарднера и многое другое Кроссворды и головоломки, Всеукраинская газета, Киев Клуб ценителей головоломок "Диоген": заочные конкурсы G4G4.com, головоломки.
Что ещё можно почитать: Кордемский Б.А. Математическая смекалка. Лёвшин В.А. Магистр Рассеянных Наук. Аменицкий Н.Н., Сахаров И.П. Забавная арифметика. Баше К. Игры и задачи, основанные на математике. Олехник С.Н., Нестеренко Ю.В., Потапов М.Н. Старинные занимательные задачи. Гарднер М. Математические чудеса и тайны. Гершензон М.А. Головоломки профессора Головоломки. Дьюдени Г.Э. 520 головоломок. Игнатьев Е.И. В царстве смекалки. Лойд С. Математическая мозаика. Люкас Э. Математические развлечения. Попов Г.Н. Памятники математической старины в задачах. Смаллиан Р.М. Принцесса или тигр? Наиболее полную библиографию можно посмотреть по адресу http://suhin.narod.ru/bibl8.htm |
http://www.math.md/school/zanimat/problemer/proble...
Задачи-шутки
Будем условно считать, что если человек не будет семь суток есть или семь суток спать, то он умрет. Пусть человек неделю не ел и не спал. Что он должен сделать в первую очередь к концу седьмых суток: поесть или поспать, чтобы остаться в живых?
(Несмотря на шутливый характер, задача имеет строгое и единственное решение).
Ответ
Снесли вместе 7 стожков сена и 11 стожков. Сколько стожков получилось?
Ответ
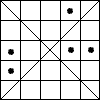
Каждую из пяти шашек передвиньте на одну клетку так, чтобы в итоге в каждом ряду, столбце и по диагоналям находилась одна шашка.
Задумайте число и запишите его. Удвойте его и прибавьте 1. Затем умножьте на 5 и вычтите 5. Разделите на 10. Результат запишите рядом с задуманным числом. Что получилось?
Ответ
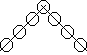
Вставьте в кружочки на рисунке числа от 1 до 7 так, чтобы на каждой прямой сумма чисел равнялась 15. (Решение задачи не единственно).
На одном доме четыре дымовые трубы, на соседнем три и на следующем две. Что получается в результате?
Ответ
Как правильно сказать: "9 и 7 будет 15" или "9 плюс 7 равно 15"?
Ответ
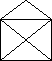
Нарисуйте этот конверт, не отрывая карандаша от бумаги.
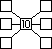
Заполните пустые клеточки на рисунке числами 2, 4, 8, 12, 16, 18 так, чтобы сумма чисел, соединенных прямыми по всем направлениям, равнялась 30. (Решение задачи не единственно).
Задумайте число и запишите его, умножьте на 5, прибавьте 2, умножьте на 4 и затем прибавьте 3. Теперь умножьте на 5 и прибавьте еще 7. Запишите результат. Вычеркните две последние цифры. Какое число получилось?
Ответ
У мальчика сестер столько же, сколько и братьев. Но у каждой сестры братьев в 2 раза больше, чем сестер. Сколько всего детей в семье? Сколько из них мальчиков и сколько девочек?
Ответ
Числа 9, 16, 23, 30, 37, 44, 51, 58, 65 необходимо расположить в магическом квадрате так, чтобы сумма чисел по каждой вертикали, горизонтали и диагонали была одинакова.
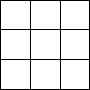
Как из 45 (сумма, которая составляется из сложения чисел от 1 до 9) вычесть 45, чтобы в итоге получилось... 45?
Ответ
Электропоезд едет с востока на запад. Набрав скорость, поезд делает 60 км/ч. В том же направлении – с востока на запад – дует ветер, но со скоростью 50 км/ч. В какую сторону относит дым поезда?
Ответ
Из 12 палочек сложили 5 квадратов. Уберите две палочки так, чтобы остались только два разных по величине квадрата.

Предположим, что земной шар охвачен по экватору обручем, который по длине превосходит экватор на 10 метров. Допустим, что обруч на всем протяжении равно удален от поверхности земли. Как велик промежуток между поверхностью и обручем? Смогла бы, скажем, проползти под обручем муха?
Ответ
Петя говорит другу: "Я поймал много больших рыб, а маленьких вдвое меньше. Всего у меня было 16 рыб." Верно ли это?
Ответ
Составьте примеры с ответом 100. При этом можно пользоваться математическими знаками +, –, ×, / :
а) пять раз цифрой 1 ;
б) четыре раза цифрой 9 ;
в) пять раз цифрой 5 .
Например, "пять раз цифрой 3" : 33×3+3/3 = 100.
Ответ
В знойный летний день, когда воздух звенит от насекомых, на зеленой лужайке площадью в три с половиной га пасутся две лошади одной породы и масти, различающиеся между собой разве только тем, что у одной хвост подвязан, а у другой – нет. Лужайка имеет форму параллелограмма, и одна из лошадей щиплет траву, передвигаясь по его диагонали, а другая – по его сторонам. Какая из этих лошадей в течение часа съест больше травы, если аппетит у них одинаков, одинаков и травяной покров лужайки, на которой они пасутся?
Ответ
Восемь чисел 1, 2, 3, 4, 6, 7, 8, 9 необходимо так расставить по квадратикам, чтобы каждая из четырех сумм (в наружном и внутреннем квадратах, а также по диагоналям) составляла 20.
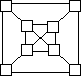
Мельник пришел на мельницу. В каждом из четырех углов он увидел по 3 мешка, на каждом мешке сидело по 3 кошки, а каждая кошка имела при себе троих котят. Спрашивается, много ли ног было на мельнице?
Ответ
Как можно одним мешком пшеницы, смоловши ее, наполнить два мешка, которые столь же велики, как и мешок, в котором находится пшеница?
Ответ
Переложите одну из палочек так, чтобы равенство было верным:
а)
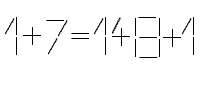
б)
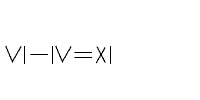
Двое прошли – три гвоздя нашли,
Следом четверо пройдут – много ли гвоздей найдут?
Ответ
Летели утки: одна впреди и две позади, одна позади и две впереди, одна между двумя и три в ряд. Сколько всего летело уток?
Ответ
Два землекопа выкапывают 2 м канавы за 2 ч. Сколько землекопов за 5 ч выкопают 5 м канавы?
Ответ
Два отца и два сына поймали 3 зайцев, а досталось каждому по 1 зайцу. Спрашивается, как это могло случиться?
Ответ
Вставьте числа 1, 1, 2, 2, 3, 3, 4, 4, 5, 5, 6, 6, 7, 7, 8, 8 в клетки магического квадрата так, чтобы сумма в каждом ряду и столбце равнялась 18.

Написать цифрами число, состоящее из одиннадцати тысяч, одиннадцати сотен и одиннадцати единиц.
Ответ
Что это такое: две ноги сидели на трех, а когда пришли четыре и утащили одну, то две ноги схватили три, бросили их в четыре, чтобы четыре оставили одну?
Ответ
Что это может быть: две головы, две руки и шесть ног, а при ходьбе только четыре?
Ответ
Как найти задуманное четное число?
Предложите кому-нибудь задумать четное число, затем это число утроить, полученное произведение разделить на 2, а частное опять утроить. После объявления результата арифметических действий вы называете задуманное число. Как это сделать?
Ответ
Как отгадать два числа?
Предложите кому-нибудь задумать два числа, одно из которых превышает другое на 1, и каждое из которых не больше девяти. Затем попросите перемножить два этих числа, из произведения вычесть меньшее из чисел и результат опять умножить на меньшее из задуманных чисел. По объявленной последней цифре полученного результата вы можете назвать задуманные числа. Как их найти?
Ответ
Как найти задуманное число?
Предложите кому-нибудь задумать не очень большое число и умножить его на само себя. К полученному результату попросите прибавить удвоенное задуманное число и еще 1. По объявленному результату арифметических действий вы можете назвать задуманное число. Как это сделать?
Ответ
Как найти цифру?
Записав число, сумма цифр которого делится на 9, и отвернувшись, предложите кому-нибудь умножить его на любое число. В полученном произведении предложите зачеркнуть любую из цифр, кроме нуля, а оставшиеся цифры переставить в произвольном порядке. После объявления результата указанных действий вы можете указать, какая цифра была зачеркнута. Как найти зачеркнутую цифру?
Ответ
Как найти зачеркнутую цифру?
Предложите кому-нибудь записать любое многозначное число, не все цифры которого одинаковы. Попросите переставить цифры этого числа таким образом, чтобы получилось число, отличное от первоначального, и записать его. Затем предложите вычесть меньшее число (из двух полученных) из большего числа, в разности зачеркнуть любую цифру, отличную от нуля, найти сумму оставшихся цифр и сказать результат. По объявленному результату вы можете сказать, какая цифра была вычеркнута. Как ее определить?
Ответ
Быстрое сложение.
Предложите кому-нибудь записать несколько чисел, имеющих одинаковое количество цифр. К этим числам вы еще дописываете несколько чисел. Сразу объявив результат, вы предлагаете найти сумму всех записанных чисел. Какие числа необходимо дописать и как быстро найти сумму всех чисел?
Ответ
Какие часы лучше?
Творчество известного английского писателя и математика Льюиса Кэрролла (Чарльза Лутвиджа Доджсона), чьи произведения читают все от мала до велика, может послужить источником популяризации логики, в том числе и математической.
Льюис Кэрролл предложил следующую задачу. Предположим, что у вас имеются двое часов, одни, которые вообще не идут, и вторые, которые отстают на одну минуту в сутки. Спрашивается, какие часы лучше?
Ответ



Новости
Добро пожаловать в Мир дистанционных конкурсов!
Проект "Мир конкурсов" с 2007 года является одним из лидеров в сфере организации и проведения дистанционных интеллектуальных и творческих состязаний на территории России и стран ближнего зарубежья. http://www.mir-konkursov.ru/