Математический клуб "Пифагор"
Сайт математического клуба "Пифагор"
С сентября 2019 года в школе работает математический клуб "Пифагор".
Задание на 08.04.2020 г. - в разделе "Литература для чтения" изучить методические рекомендации по решению задач на движение и решить задачи № 1-5 из Дидактических материалов (расположены ниже, в этом же разделе).
Задание на 15.04.2020 г.- в разделе "Литература для чтения" изучить методические рекомендации по решению задач на производительность и работу. Решить задачи № 3-8 из Дидактических материалов ( расположены ниже, в этом же разделе).
Задание на 11.11.2020 г. - в разделе "Литература для чтения" изучить методические рекомендации по теме "Множества и их элементы. Подмножества. Операции над множествами". Выполнить домашнее задание- решить 5 задач по теме.
Задание на 18.11.2020 г. - в разделе"Литература для чтения" изучить методические рекомендации по теме "Парадоксы в логике. Парадокс брадобрея. "
Задание на 25.11.2020 г. - в разделе "Литература для чтения" изучить методические рекомендации по теме "Определение модуля числа и его применение при решении уравнений." Решить уравнения для самостоятельной работы.
Задание на 02.12.2020 г. -в разделе "Литература для чтения" изучить методические рекомендации по теме " Метод интервалов решения уравнений и неравенств, содержащих модуль".Решить уравнения для самостоятельной работы.
Задание на 09.12.2020 г.- в разделе "Литература для чтения" изучить методические рекомендации по теме "Решение неравенств вида ׀х׀<а ׀х׀>а посредством равносильных переходов." Решить уравнения для самостоятельной работы.
Руководитель кружка - Ефремова Вера Владимировна
Занятия кружка проходят по средам с 15.30 до 17.00 ч.
- Если, а>0, то |а|=а (|5| =5);
- Если, а=0, то |а| =а (|0|=0);
- Если, а<0, то |а|=-а (|-3|=-(-3)=3).
- |3х + 1|=7;
- |1 – 2х|=43;
- |11 + 10х|=1;
- |7 – 3х|=11.
- |2х - 7|≤2;
- |18 - х| ≥ 48;
- |1 + 5х| < 4;
- |2 – 9х|>13.
- |2х + 1| >5;
- |3 – 2х|<3;
- 1/|х - 3| > 1.
- ||х| - 6| = 5.
- |х - 3|=|х+ 5|.
- |х - 3| + |х - 5| > 3.
- ||2х + 4| - 7| - 13 ≤ 2с2 удовлетворяет условию х [-37; 35].
Метод интервалов решения уравнений и неравенств, содержащих модуль.
Метод интервалов позволяет решать любые уравнения, содержащие модуль. Суть этого метода в том, чтобы разбить числовую ось на несколько участков (интервалов), причем разбить ось нужно именно нулями выражений, стоящих в модулях. Затем на каждом из получившихся участков всякое подмодульное выражение либо положительно, либо отрицательно. Поэтому каждый из модулей может быть раскрыт или со знаком минус, или со знаком плюс. После этих действий остается лишь решить каждое из полученных простых уравнений на рассматриваемом интервале и объединить полученные ответы.
Рассмотрим данный метод на конкретном примере.
|x + 1| + |2x – 4| – |x + 3| = 2x – 6.
1) Найдем нули выражений, стоящих в модулях. Для этого нужно приравняем их к нулю, и решить полученные уравнения.
x + 1 = 0 2x – 4 = 0 x + 3 = 0
x = -1 2x = 4 x = -3
x = 2
2) Расставим получившиеся точки в нужном порядке на координатной прямой. Они разобьют всю ось на четыре участка.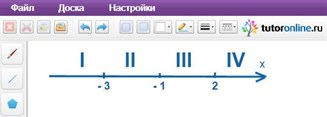
3) Определим на каждом из получившихся участков знаки выражений, стоящих в модулях. Для этого подставляем в них любые числа с интересующих нас интервалов. Если результат вычислений – число положительное, то в таблице ставим «+», а если число отрицательное, то ставим «–». Это можно изобразить так: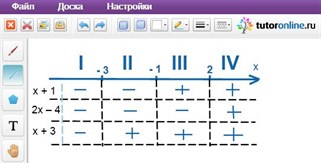
4) Теперь будем решать уравнение на каждом из четырех интервалов, раскрывая модули с теми знаками, которые проставлены в таблице. Итак, рассмотрим первый интервал:
I интервал (-∞; -3). На нем все модули раскрываются со знаком «–». Получим следующее уравнение:
-(x + 1) – (2x – 4) – (-(x + 3)) = 2x – 6. Приведем подобные слагаемые, раскрыв предварительно скобки в полученном уравнении:
-x – 1 – 2x + 4 + x + 3 = 2x – 6
-4x = -12
x = 3.
Полученный ответ не входит в рассматриваемый интервал, поэтому в окончательный ответ писать его не надо.
II интервал [-3; -1). На этом интервале в таблице стоят знаки «–», «–», «+». Именно так и раскрываем модули исходного уравнения:
-(x + 1) – (2x – 4) – (x + 3) = 2x – 6. Упростим, раскрыв при этом скобки:
-x – 1 – 2x + 4 – x – 3 = 2x – 6. Приведем в полученном уравнении подобные:
-5x = -6
x = 6/5. Полученное число не принадлежит рассматриваемому интервалу, поэтому оно не является корнем исходного уравнения.
III интервал [-1; 2). Раскрываем модули исходного уравнения с теми знаками, которые стоят на рисунке в третьей колонке. Получаем:
(x + 1) – (2x – 4) – (x + 3) = 2x – 6. Избавимся от скобок, перенесем слагаемые, содержащие переменную x в левую часть уравнения, а не содержащие x в правую. Будем иметь:
x + 1 – 2x + 4 – x – 3 = 2x – 6
-4x = -8
x = 2.
В рассматриваемый интервал число 2 не входит.
IV интервал [2; +∞). Все модули раскрываем со знаком «+». Получим:
(x + 1) + (2x – 4) – (x + 3) = 2x – 6.
x + 1 + 2x – 4 – x – 3 = 2x – 6
0 = 0.
После преобразований уравнение превратилось в верное равенство. Это говорит о том, что любое число из рассматриваемого интервала будет являться решением исходного уравнения. Значит ответом, как на этом интервале, так и во всем уравнении является множество чисел, удовлетворяющих условию x ≥ 2.
Ответ: x ≥ 2.
Решение неравенств вида ׀х׀<а ׀х׀>а посредством равносильных переходов.
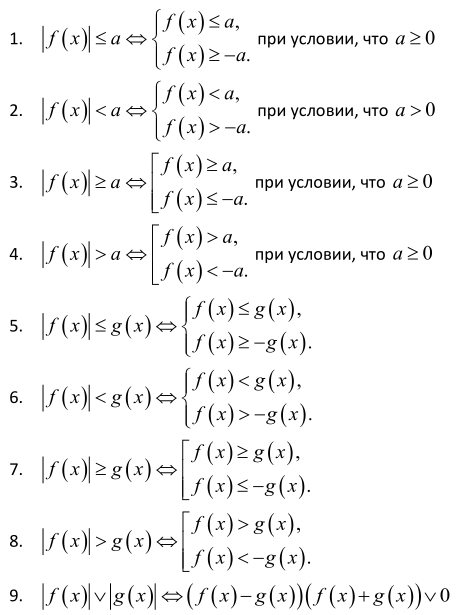
Парадоксы в логике. Парадокс брадобрея
 "To shave or not to shave…" |
Это довольно известная история, и у нее есть много версий.
В одном полку жил-был полковой парикмахер, которого по историческим причинам называют брадобреем. Однажды командир приказал ему брить тех и только тех, кто не бреется сам*5. Брадобрей, получив приказ, сначала обрадовался, потому что многие солдаты умели бриться сами, побрил тех, кто бриться сам не умел, а потом сел на пенек и задумался: а что ему с собой-то делать? Ведь если он будет брить себя, то нарушит приказ командира не брить тех, кто бреется сам. Брадобрей уже решил было, что брить себя не будет. Но тут его осенила мысль, что если он сам себя брить не будет, то окажется, что он сам не бреется, и по приказу командира он должет все-таки себя побрить…
| *5 Приказ довольно разумный: если солдат бреется сам, то зачем тратить на него время полковому парикмахеру? Наверное, полк был большой, и брадобрей просто не справлялся. |
Что с ним стало, история умалчивает.
Причем же здесь теория множеств? А вот причем: командир пытался определить множество людей, которых брадобрею нужно брить, таким образом:
те и только те, кто не бреется сам
.
Казалось бы, обычное множество, описывается несколькими русскими словами, чем оно хуже, например, множества
все ученики школы
?
Но с этим множеством тут же возникает проблема: непонятно, принадлежит ли этому множеству брадобрей.
Вот другая версия этого парадокса.
Прилагательное русского языка назовем рефлексивным, если оно обладает свойством, которое определяет. Например, прилагательное "русский" — рефлексивное, а прилагательное "английский" — нерефлексивное, прилагательное "трехсложный" — рефлексивное (это слово состоит из трех слогов), а прилагательное "четырехсложный" — нерефлексивное (состоит из пяти слогов)*6. Вроде бы ничто не мешает нам определить множество
все рефлексивные прилагательные
.
Но давайте рассмотрим прилагательное "нерефлексивный". Оно рефлексивное или нет?
| *6 Интересно, а прилагательное "трудновыговариваемое" является рефлексивным? |
Можно заявить, что прилагательное "нерефлексивный" не является ни рефлексивным, ни нерефлексивным. Но как тогда быть с таким заклинанием:
верно либо утверждение, либо его отрицание?
(Это заклинание называется законом исключенного третьего; на нем, собственно, и основан метод от противного.)
Наконец, третья версия парадокса. Рассмотрим множество
=
множества
, такие что
— мы включаем во множество только те множества
, которые принадлежат сами себе. Бывают же множества, которые содержат другие множества. Например, пусть
,
,
множеству принадлежат числа
, а множеству
— два элемента: множество
и число
. Возвращаясь к коробкам, это можно сказать так: одни коробки можно класть в другие коробки. (Оказывается, что в каждой такой последовательности вложенных коробок всегда конечное число элементов — этому есть глубокие причины.)
Рассмотренное множество — это своего рода "брадобрей". Если предположить, что
, сразу приходим к выводу, что
. Если же предположить, что
— получаем, что
.
Столкнувшись с этими парадоксами, создатели теории множеств осознали, что нельзя задавать множества произвольными словосочетаниями. После этого они стали бороться с парадоксами двумя способами.
Первый способ — способ Кантора, придумавшего "наивную теорию множеств", в которой запрещаются все действия и операции, ведущие к парадоксам. Идея в следующем: разрешается работать со множествами, которые " встречаются в природе", также разрешается работать со множествами, которые получаются из них разумными теоретико-множественными операциями. Пусть, например,
=
множество учащихся школы
,
=
множество непрерывных функций
(эти множества "встречаются в природе"), из них можно получить объединение , пересечение
. Можно даже умножить множество
на множество
: по определению
— множество пар, в которых первый элемент из первого множества, а второй — из второго. В нашем случае — это множество пар, в которых первый элемент — учащийся школы, а второй — какая-нибудь непрерывная функция.
Другой способ — аксиоматический. Этот способ преодоления парадоксов развивали Цермело и Френкель (система аксиом Цермело–Френкеля), Гедель и Бернайс (система аксиома Геделя–Бернайса). Согласно этой теории, множество — это нечто, удовлетворяющее аксиомам, например, следующим{1}.
Записи аксиом дублируются на "языке кванторов". Вот значения используемых кванторов: — для любого
;
— существует
;
— существует единственный
;
—
является множеством;
— множество тех и только тех
, которые удовлетворяют условию
;
— логическое "или";
— логическое "и".
1. Аксиома объемности. Множество определяется своими элементами: множества, состоящие из одних и тех же элементов, равны.
.
2. Аксиома объединения. Объединение всех элементов множества есть множество.
.
3. Аксиома выделения. Для каждого множества и каждого условия
существует множество
— подмножество элементов множества , удовлетворяющих условию
.
Другими словами, мы не можем взять множество всех летающих крокодилов со всего мира или множество тех множеств, которые не содержат сами себя, а можем, взяв некоторое множество, выделить в нем "кусочек" — множество его элементов, удовлетворяющих некоторому условию.
.
4. Аксиома степени. Множество всех подмножеств данного множества есть множество.
.
5. Аксиома подстановки. Пусть — множество, а
— произвольная формула. Тогда если для каждого
существует и единственен
, такой что истинно
, то существует множество всех
, для которых найдется
, такой что
истинно.
.
6. Аксиома фундирования. Не существует бесконечной последовательности вложенных множеств: каждая цепочка множеств
конечна.
.
7. Аксиома бесконечности. Существуют бесконечные множества, т. е. такие множества , что
равномощно
.
.
8. Аксиома выбора. Еще одна очень сложная, но и очень очевидная аксиома
Понятие множества. Подмножества. Операции над множествами. Алгебра множеств.
Т.е., можно сказать, что множество – это определенная совокупность различных объектов (предметов или понятий), объединенных в одно целое. Объекты. Обычно множества обозначают прописными латинскими буквами, а их элементы – Конечное множество можно задать перечислением его элементов. При задании множества в форме списка непосредственно.
Подмножества.
Каждое непустое множество имеет по крайней мере два подмножества: 1) пустое множество является подмножеством любого множества Æ ; 2) каждое множество является подмножеством самого себя .
Операции над множествами
3.1 Объединением ( суммой) двух множеств  и
и  называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из данных множеств. Объединение записывается как
называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из данных множеств. Объединение записывается как
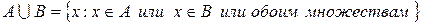 .
.
Пример.
Пусть 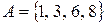 и
и 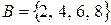 . Тогда объединение
. Тогда объединение  и
и  есть
есть 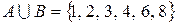 . При этом элементы 6 и 8 принадлежат обоим множествам.
. При этом элементы 6 и 8 принадлежат обоим множествам.
Аналогично определяется объединение более чем двух множеств. Объединение трех множеств  ,
,  и
и 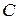 есть множество
есть множество 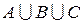 , каждый, из элементов которого принадлежит хотя бы одному из множеств
, каждый, из элементов которого принадлежит хотя бы одному из множеств  ,
,  и
и 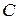 :
:
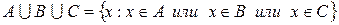 .
.
3.2 Пересечением (произведением) двух множеств  и
и  называется новое множество,состоящее из всех элементов, одновременно принадлежащих каждому из данных множеств
называется новое множество,состоящее из всех элементов, одновременно принадлежащих каждому из данных множеств  и
и  .
.
Пересечение записывается как 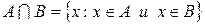 .
.
Пример. Пусть 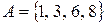 и
и 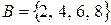 . Тогда
. Тогда 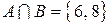 .
.
Пересечение более чем двух множеств определяется аналогичным образом. Пересечение трех множеств  ,
,  и
и 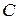 есть множество элементов, которые принадлежат
есть множество элементов, которые принадлежат  ,
,  и
и 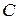 :
: 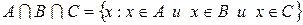 .
.
Если множества  и
и  не имеют общих элементов, то их пересечение пусто:
не имеют общих элементов, то их пересечение пусто: 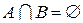 . Такие множества
. Такие множества  и
и  называются непересекающимися.
называются непересекающимися.
Пример. Пусть  – множество целых положительных чисел, а
– множество целых положительных чисел, а  – множество целых отрицательных чисел. Тогда
– множество целых отрицательных чисел. Тогда  и
и  – непересекающиеся множества, так как не существует целых чисел, которые были бы одновременно и положительными, и отрицательными.
– непересекающиеся множества, так как не существует целых чисел, которые были бы одновременно и положительными, и отрицательными.
Определение непересекающихся множеств может быть распространено на случай более чем двух множеств.
Говорят, что 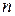 множеств
множеств 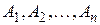 являются взаимно непересекающимися (или попарно непересекающимися), если никакие два из этих множеств не имеют общих элементов. Иными словами, множества
являются взаимно непересекающимися (или попарно непересекающимися), если никакие два из этих множеств не имеют общих элементов. Иными словами, множества 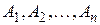 взаимно непересекающиеся, если
взаимно непересекающиеся, если 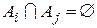 при
при 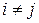 для
для 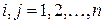 .
.
3.3 Разбиение множества на подмножества. В основе всевозможных классификаций, применяемых в биологии, лингвистике и других науках, лежит операция разбиения множества на попарно непересекающиеся подмножества. Одно и то же множество можно разбивать на подмножества разными способами: совокупность людей можно разделить на детей и взрослых, на мужчин и женщин.
Разбиение множества  есть набор его подмножеств
есть набор его подмножеств 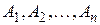 , которые взаимно не пересекаются и в объединении дают
, которые взаимно не пересекаются и в объединении дают  . Это записывается так:
. Это записывается так: 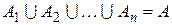 и
и 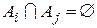 при
при 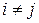 для
для 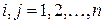 .
.
Пример. 1) Множество натуральных чисел разбивается на подмножества четных и нечетных чисел. 2) Множество всех многоугольников разбивается на множества треугольников, четырехугольников, пятиугольников и т.д.
3.4 Разностью двух множеств  и
и  называется множество, элементами которого являются те и только те элементы множества
называется множество, элементами которого являются те и только те элементы множества  , которые не принадлежат
, которые не принадлежат  . При этом предполагается, что множество
. При этом предполагается, что множество  не является частью множества
не является частью множества  . Разность множеств
. Разность множеств  и
и  обозначается
обозначается 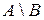 и по определению
и по определению 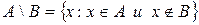 . Таким образом, при вычитании множества
. Таким образом, при вычитании множества  из множества
из множества  из
из  удаляют пересечение
удаляют пересечение  и
и  :
: 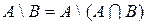 .
.
Пример.
1) Пусть  – множество студентов данной группы института,
– множество студентов данной группы института,  – множество девушек, обучающихся в этом институте. Тогда
– множество девушек, обучающихся в этом институте. Тогда 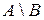 – множество всех юношей, обучающихся в данной группе этого института.
– множество всех юношей, обучающихся в данной группе этого института.
2) Пусть 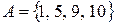 ,
, 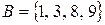 . Тогда
. Тогда 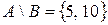 и
и 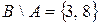 .
.
3.5В случае, когда  – часть множества
– часть множества  ,
, 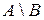 называют дополнением к
называют дополнением к  в множестве
в множестве  и обозначают
и обозначают 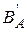 .
.
Пример. Пусть  – множество четных чисел,
– множество четных чисел,  – множество целых чисел. Тогда
– множество целых чисел. Тогда 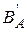 – множество нечетных чисел.
– множество нечетных чисел.
3.6 Часто все множества, с которыми имеют дело в том или ином рассуждении, являются подмножествами некоторого определенного фиксированного множества. Это множество называют универсальным и обозначают 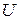 .
.
Дополнением множества  по отношению к универсальному множеству
по отношению к универсальному множеству 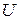 есть множество
есть множество 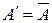 , составленное из всех тех элементов
, составленное из всех тех элементов 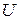 , которые не находятся в
, которые не находятся в  :
:
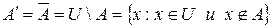 .
.
Пример. Для учебной группы института определим  как множество всех юношей этой группы, а
как множество всех юношей этой группы, а  – как множество студентов группы, сдавших экзамены. Универсальным множеством
– как множество студентов группы, сдавших экзамены. Универсальным множеством 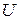 является множество всех студентов этой группы. Тогда
является множество всех студентов этой группы. Тогда 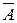 – множество девушек этой группы;
– множество девушек этой группы; 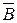 – студенты, не сдавшие экзамены;
– студенты, не сдавшие экзамены; 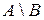 – юноши, не сдавшие экзамены;
– юноши, не сдавшие экзамены; 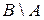 – девушки, сдавшие экзамены.
– девушки, сдавшие экзамены.
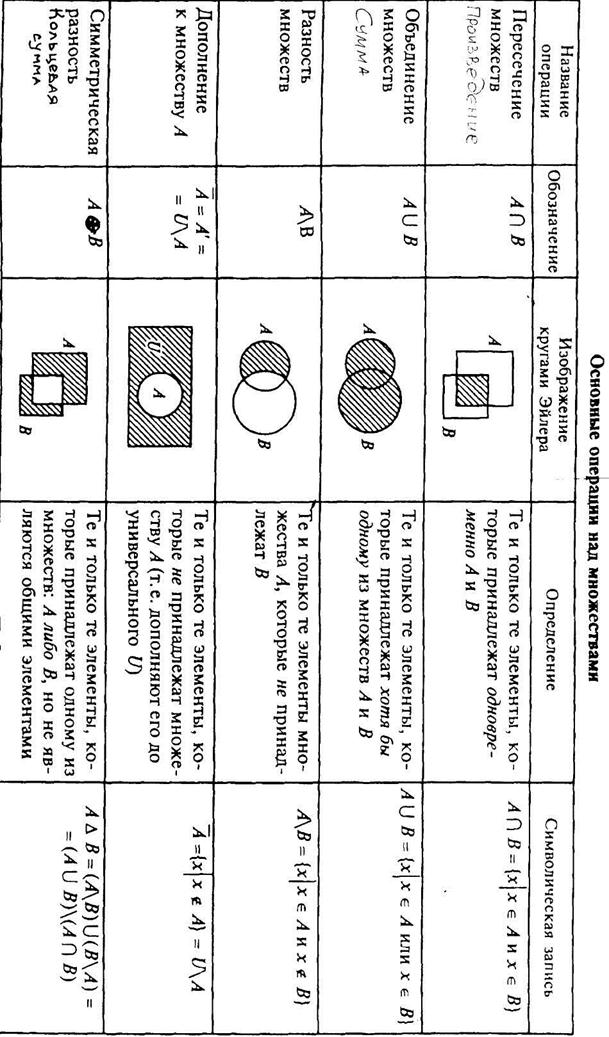
Для наглядного изображения множеств и их свойств используются диаграммы Эйлера–Венна. В этом случае множество будем изображать кругом на плоскости, и представлять элементы множества как множество точек круга. Универсальное множество 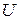 будем изображать множеством точек некоторого прямоугольника. Если изобразить кругами множества
будем изображать множеством точек некоторого прямоугольника. Если изобразить кругами множества  и
и  , то множества
, то множества 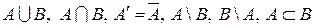 изобразятся следующими заштрихованными областями:
изобразятся следующими заштрихованными областями:
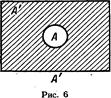
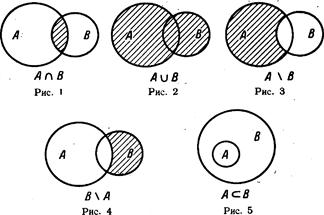
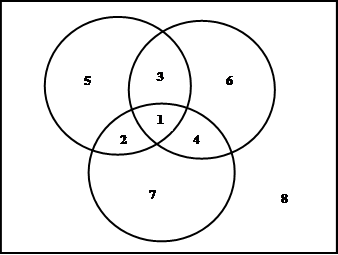
Для случая трех множеств на рисунке представлены все восемь возможностей принадлежности некоторого элемента трем данным множествам. Область, отмеченная цифрой 1, изображает множество элементов, принадлежащих всем трем множествам. Элементы, принадлежащие только двум из трех данных множеств, попадают в области 2, 3, 4, а элементы, принадлежащие только одному из трех данных множеств, попадают в области 5, 6 и 7. Множество элементов, не принадлежащих ни одному из трех данных множеств, соответствует внешней области, отмеченной цифрой 8. Все возможности принадлежности элемента трем данным множествам исчерпаны.
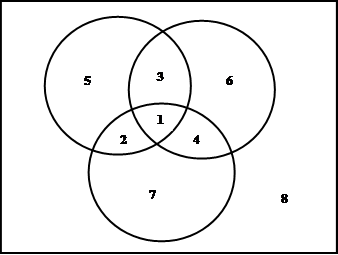 |
Теория нечетких множеств (fuzzy sets theory) ведет свое начало с 1965г., когда профессор Лотфи Заде (Lotfi Zadeh) из университета Беркли опубликовал основополагающую работу “Fuzzy Sets” в журнале “Information and Control”. Прилагательное "fuzzy", которое можно перевести на русский как нечеткий, размытый, ворсистый, пушистый, введено в название новой теории с целью дистанцирования от традиционной четкой математики и Аристотелевой логики, оперирующих с четкими понятиями: “принадлежит - не принадлежит”, “истина - ложь”. Концепция нечеткого множества зародилась у Заде “как неудовлетворенность математическими методами классической теории систем, которая вынуждала добиваться искусственной точности, неуместной во многих системах реального мира, особенно в так называемых гуманистических системах, включающих людей”.
Началом практического применения теории нечетких множеств можно считать 1975 г., когда Мамдани и Ассилиан (Mamdani and Assilian) построили первый нечеткий контролер для управления простым паровым двигателем. В 1982 Холмблад и Остергад (Holmblad and Osregaad) разработали первый промышленный нечеткий контроллер, который был внедрен в управление процессом обжига цемента на заводе в Дании. Успех первого промышленного контролера, основанного на нечетких лингвистических правилах “Если - то” привел к всплеску интереса к теории нечетких множеств среди математиков и инженеров. Несколько позже Бартоломеем Коско (Bart Kosko) была доказана теорема о нечеткой аппроксимации (Fuzzy Approximation Theorem), согласно которой любая математическая система может быть аппроксимирована системой, основанной на нечеткой логике. Другими словами, с помощью естественно-языковых высказываний-правил “Если - то”, с последующей их формализацией средствами теории нечетких множеств, можно сколько угодно точно отразить произвольную взаимосвязь “входы-выход” без использования сложного аппарата дифференциального и интегрального исчислений, традиционно применяемого в управлении и идентификации.
Системы, основанные на нечетких множествах разработаны и успешно внедрены в таких областях, как: управление технологическими процессами, управление транспортом, медицинская диагностика, техническая диагностика, финансовый менеджмент, биржевое прогнозирование, распознавание образов. Спектр приложений очень широкий - от видеокамер и бытовых стиральных машин до средств наведения ракет ПВО и управления боевыми вертолетами. Практический опыт разработки систем нечеткого логического вывода свидетельствует, что сроки и стоимость их проектирования значительно меньше, чем при использовании традиционного математического аппарата, при этом обеспечивается требуемый уровень робастности и прозрачности моделей.
Эпиграф:
Множество возникает путем объединения
отдельных предметов в единое целое.
Оно есть множественность мыслимая как единое.
Ф. Хаусдорф
Множество представляет собой объединение некоторых объектов или предметов в единую совокупность по каким-либо общим свойствам или законам.Обозначают А,В,Р,…
Например:
множество зверей,
множество учеников;
множество столов;
множество стульев;
Предметы, составляющие данное множество, называются его элементами.
Обозначают .
Если множество А состоит из элементов a , c , k , то записывают это так: А = { a , c , k }.
Например, множество дней недели состоит из элементов: понедельник, вторник, среда, четверг, пятница, суббота, воскресенье.
Множество месяцев – из элементов: январь, февраль, март, апрель, май, июнь, июль, август, сентябрь, октябрь, ноябрь, декабрь.
Множество арифметических действий - из элементов: сложение, вычитание, умножение, деление.
Множества, состоящие из чисел, называют числовыми множествами.
N – множество натуральных чисел,
Z – множество целых чисел.
Виды множеств

Подмножество
Если каждый элемент множества В является элементом множества А, то множество В называется подмножеством множества А.
Пустое множество, по определению, считают подмножеством всякого множества.Обозначают Ø
Если два множества состоят из одних и тех же элементов, то они называются равными.
Например, А = { a , c , k , m , n } и В = { m , n , a , c , k }, А = В.
Множество является заданным, т.е. известным, если ясно, какие у него элементы. Поэтому, чтобы задать множество, можно просто перечислить все его элементы.
Круги́ Э́йлера[— геометрическая схема, с помощью которой можно изобразить отношения междуподмножествами, для наглядного представления. Изобретены Леонардом Эйлером.
При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов.
Однако, этим методом ещё до Эйлера пользовался выдающийся немецкий философ и математик Готфрид Вильгельм Лейбниц (1646—1716). Практическая работа
Задание1
Перечислите множество фруктов
Перечислите множество овощей
Перечислите множество школьных предметов учеников 6 класса
Задание 2
Начертите три круга изображающие круги Эйлера. В самом маленьком круге напишите, те знания и умения которые вы приобрели в дошкольном возрасте (множества А), во втором круге – чем пополнились ваши знания в начальной школе (множества В) и в самом большом круге чему вы научились в 5-6 классах (множество С). В каком отношении находятся эти множества? (ответ А подмножества множества В и в – подмножества множества С)
1.Дано множество {11; 34; 60; 16; 90}. Принадлежит ли этому множеству число, которое получится при сложении 60 и 30, при вычитании 9 из 17, при делении 72 на 8, при вычитании И из 48, при умножении 20 на 3? [да; нет; нет; да; да].
2.По какому признаку составлено множество {зима, весна, лето, осень}, {11. 13, 15, 17, 19}? [времена года, [нечетные числа большие 10 и меньшие 20].
3.По какому признаку составлено множество {6,3,5,2,4}? [Множество чисел, больших 1 и меньших 7. Является ли это мно жество подмножеством натуральных чисел? [Да].
4.Назовите множество дней одной недели; множество месяцев одного года. Является ли множество дней одной недели подмно жеством множества дней одного месяца? [Да].
5.Даны следующие множества:
А - множество учеников данной школы;
В - множество учеников пятых классов данной школы;
С - множество учащихся всех школ данного города;
Д - множество учащихся пятых классов, посещающих кружковые занятия по математике;
Е - множество всех учащихся школ России.
[ Д ВАСЕ].
Перечислить буквы, обозначающие множества, так, чтобы каждая буква (кроме последней) обозначала подмножество следующего множества.
6.Даны множества:
А - множество натуральных чисел;
В - множество четных чисел;
С - множество нечетных чисел;
Д - множество чисел, делящихся на 5;
Е - множество чисел, делящихся на 10.
[ВА, СА, ДА, ЕА, ДС, ЕВ, ДЕ].
Указать, какие из данных множеств являются подмножествами других данных множеств.
7.Назовите множество натуральных чисел, расположенных между числами 21 и 22.
[Ø]
Часть 2.Решим ЗАДАЧУ № 1.
«В пятых классах школы училось 70 человек. Им было предложено записаться в 3 кружка: по математике, литературе и истории. Староста подсчитал число учащихся, желающих участвовать во внеклассной работе, и получил такие результаты. В кружок по математике записалось 51 человек, по литературе - 40, по истории - 22. 6 человек решили заниматься во всех кружках, математикой и литературой решили заниматься 32 человека, одновременно заниматься математикой и историей решили 11 человек, а литера турой и историей 8 человек. Получив результаты, староста сказал: «Можно подумать, что у нас в 5-х классах обучается не 70 человек, а 170. Все хотят заниматься в кружках».
Однако один из любителей математики сказал: «Что ты, у нас есть ученики, которые не любят ни математику, ни литературу, ни исто рию. Я даже могу сказать, сколько их». Как он узнал?»
Введем обозначения:
В - множество всех учащихся;
М — множество учащихся (кружковцев), увлекающихся мате матикой;
JI — множество учащихся (кружковцев), увлекающихся лите ратурой;
И - множество учащихся (кружковцев), увлекающихся историей.
Из условия задачи следует, что все условия пересекаются.
Для составления схемы воспользуемся «кругами Эйлера».
Пересечение множеств М, JI и Д содержит 6 элементов (МЛИ|=6 это следует из условия задачи).
Пересечение множеств М и Л содержит 32 элемента (|MЛ|=32), но 6 элементов принадлежат множеству И (смотри рисунок).
Можно определить, сколько человек записать в кружки по мате матике и литературе (32-6=26 человек).
Пересечение множеств М и И содержит 11 элемента (|МИ|=11), но 6 элементов принадлежат множеству JI; следовательно в кружки по математике и истории записалось 11-6=5 человек.
ЛИ содержит 8 человек (|ЛИ|=8), но 6 элементов принадлежат множеству М, значит в кружки по литературе и истории записалось 8-6=2 человека.
Теперь легко определить сколько учащихся посещают только один кружок:
по математике - 51-(6+26+5)= 14 человек;
по литературе - 40-(6+26+2)=6 человек;
по истории - 22-(6+5+2)=9 человек;
всего записалось — 14+6+9+26+5+6+2=68 человек;
не записалось - 70-68=2 человека.
Решим ЗАДАЧУ № 2.
«В классе 40 человек. Играют в баскетбол 26 человек, занимаются плаванием - 25, ходят на лыжах - 27. Одновременно занимаются плаванием и баскетболом - 15, баскетболом и лыжами - 16, пла ванием и лыжами - 18. Один человек освобожден от занятий по физ культуре. Сколько человек занимается всеми указанными видами спорта? Сколько человек занимается только в одной спортивной секции?».
Введем обозначения:
Л - множество лыжников;
Б - множество баскетболистов;
П - множество пловцов.
По условию задачи все три множества пересекаются. Число эле ментов пересечения трёх множеств обозначим через X.
Пересечение множеств Б и П (БП) содержит 15 человек (|БП| = 15), но X человек принадлежат множеству Л. Можно определить, сколько человек занимаются баскетболом и плава нием: 15-Х (чел.).
Пересечение множеств JI и П (ЛП) содержит 18 человек (|ЛП|=18), но X человек принадлежат множеству Б. Можно определить, сколько человек занимаются лыжами и плаванием: 18-Х (чел.).
Пересечение множеств Б и JI (БЛ) содержит 16 человек (|БЛ|= 16), но X человек принадлежат множеству П. Можно определить, сколько человек занимаются баскетболом и лыжами: 16-Х (чел.).
Теперь легко определить, сколько учащихся занимаются только баскетболом:
26-(16-Х+Х+15-Х)=26-(31 -X).
Сколько учащихся занимаются только плаванием:
25-(18-Х+Х+15-Х)=25-(33-Х).
Сколько учащихся занимаются только лыжами:
27-(16-Х+Х+18-Х)=27-(34-Х).
По условию задачи известно, что в классе 40 человек и один чело век освобожден от занятий по физкультуре. Следовательно, можно составить уравнение:
25-(33-Х)+27-(34-Х)+26-(31 -Х)+15-X+l 8-Х+16-Х+Х+1 =40.
Отсюда, Х= 10, т. е. 10 человек одновременно занимаются баскет болом, плаванием и лыжами.
26-(31-10)=5 (чел.) занимаются только баскетболом.
3 (чел.) занимаются только лыжами.
25-(33-10)=2 (чел.) занимаются только плаванием.
Задача № 3
Из 40 учащихся класса выписывают газету, 21 – журнал, 15 учащихся – и газету и журнал. Сколько учащихся не выписывают ни журнала, ни газеты?
32-15=17 (чел.) - выписывают только газету.
21-15=6 (чел.) - выписывают только журнал.
40—(15+17+6)=2 (чел.).
Ответ: 2 человека не выписывают ни газеты, ни журнала.
Задача №4
В классе 35 учеников. 20 человек посещают математический кружок, 11 – биологический. 10 человек не посещают кружков. Сколько биологов увлекается математикой?
35-10=25 (чел.) - посещают кружки.
Пусть X чел. посещают и биологический, и математический кружки, тогда 20-Х (чел.) - посещают математический кружок, а 11 -X (чел.) - посещают биологический кружок.
Известно, что всего в кружках занимаются 25 человек. Следо вательно, можно составить уравнение:
20-Х+11-Х+Х=25
Х=6
Ответ: 6 биологов увлекаются математикой.
ЗАДАЧА №5.
Из 100 человек 85 знают английский язык, 80 – испанский, 75 – немецкий. Все владеют по крайней мере одним иностранным языком. Среди них нет таких, которые знают только два иностранных языка, но есть владеющие тремя языками. Сколько человек знают три иностранных языка?
Пусть X чел. владеют тремя языками, тогда (85-Х) чел. Владе ют только английским языком,(80-Х) чел. - только испанским, (75-Х) чел. - только немецким. По условию задачи известно, что среди 100 человек нет таких, которые знают только два иностранных языка, но все владеют по крайней мере одним иностранным языком. Следовательно, можно составить уравнение:
85-Х+Х+80-Х+75-Х=100
Х=70.
Ответ: 70 человек знают три иностранных языка.
Часть 3. Отношения между множествами. Операции над множествами. Разбиение множества на классы.
Между двумя множествами существует несколько видов отношений. Если множества А и В не имеют общих элементов, то говорят, что эти множества не пересекаются и записывают этот факт в виде А∩В =∅ . Например, А = { a , c , k }, В = { d , e , m , n }, общих элементов у этих множеств нет, поэтому множества не пересекаются.
Если множества А и В имеют общие элементы, т.е. элементы, принадлежащие одновременно А и В, то говорят, что эти множества пересекаются и записывают А∩В≠∅ . Например, множества А = { a , c , k } и В = { c , k , m , n } пересекаются, т. к. у них есть общие элементы c , k .
Множество В является подмножеством множества А, если каждый элемент множества В является также элементом множества А. Пустое множество является подмножеством любого множества. Само множество является подмножеством самого себя. (пишут В⊂ А)
Существует пять случаев отношений между двумя множествами. Их можно наглядно представить при помощи особых чертежей, которые называются кругами или диаграммами Эйлера-Венна.

а) б) в) г) д)
Определение. Пересечением множеств А и В называется множество, содержащее все элементы, которые принадлежат множеству А и множеству В.
Пересечение множеств А и В обозначают А∩ В. Таким образом, по определению, А ∩ В = { х | х ∈ А и х ∈ В}.
Например, если А = { a , c , k , m , n } и В = { a , b , c , d , e }, то А ∩ В = { a , c }.
Если изобразить множества А и В при помощи кругов Эйлера-Венна, то пересечением данных множеств является заштрихованная область (рис. 3).
Для пересечения множеств выполняются следующие свойства.
1) Переместительное или коммутативное свойство: А ∩ В = В ∩ А.
2) Сочетательное или ассоциативное свойство:(А ∩ В) ∩ С = А ∩ (В ∩ С).
3) А ∩ ∅ = ∅ (пустое множество является поглощающим элементом).
4) А ∩ U = А (универсальное множество является нейтральным элементом).
5) Если В ⊂А, то А∩В = В
Определение. Объединением множеств А и В называется множество, содержащее все элементы, которые принадлежат множеству А или множеству В.
Объединение множеств А и В обозначают А∪ В. Таким образом, по определению, А ∪ В = { х | х ∈А или х∈В}.
Например, если А = { a , c , k , m , n } и В = { a , b , c , d , e }, то А ∪ В = { a , c , k , m , n , b , d , e }.
Если изобразить А и В при помощи кругов Эйлера-Венна, то объединением данных множеств является заштрихованная область
Для объединения множеств выполняются следующие свойства.
1) Переместительное или коммутативное свойство: А ∪ В = В ∪ А.
2) Сочетательное или ассоциативное свойство:(А ∪ В)∪ С = А ∪ (В ∪ С).
3) А ∪ ∅= А (пустое множество является нейтральным элементом).
4) А ∪ U = U (универсальное множество является поглощающим элементом).
5) Если В ⊂А, то А∪В = В
Операции объединения и пересечения множеств связаны законами дистрибутивности или иначе распределительными свойствами:
(А ∪ В) ∩С = (А∩С) ∪ (В∩С) и (А∩В) ∪ С = (А ∪ С) ∩(В ∪ С).
П р и м е р 1. Пусть А – множество различных букв в слове «математика», а В – множество различных букв в слове «стереометрия». Найти пересечение и объединение множеств А и В.
Р е ш е н и е. Запишем множества А и В, перечислив их элементы: А = { м, а, т, е, и, к }, В = { с, т, е, р, о, м, и, я }. Буквы м, т, е, и принадлежат и множеству А, и множеству В, поэтому они войдут в пересечение этих множеств: А∩В = { м, т, е, и }. В объединение этих множеств войдут все элементы множества А и несовпадающие с ними элементы из множества В: А ∪ В = { м, а, т, е, и, к, с, р, о, я }.
П р и м е р 2 . В классе английский язык изучают 25 человек, а немецкий – 27 человек, причем 18 человек изучают одновременно английский и немецкий языки. Сколько всего человек в классе изучают эти иностранные языки? Сколько человек изучают только английский язык? Только немецкий язык?

Р е ш е н и е. Через А обозначим множество школьников, изучающих английский язык, через В – множество школьников, изучающих немецкий язык. Изобразим эту ситуацию с помощью диаграммы. Два языка изучают 18 школьников, поставим это число в пересечение множеств А и В. Английский язык изучают 25 человек, но среди них 18 человек изучают и немецкий язык, значит, только английский язык изучают 7 человек, укажем это число на диаграмме. Рассуждая аналогично, получим, что только немецкий язык изучают 27 – 18 = 9 человек. Поместим и это число на диаграмму. Теперь известно количество элементов в каждой части множеств, изображенных на диаграмме. Чтобы ответить на главный вопрос задачи, нужно сложить все числа: 7 + 18 + 9 = 34. Ответ: 34 человека в классе изучают иностранные языки.
Определение. Разностью множеств А и В называется множество, содержащее те и только те элементы, которые принадлежат множеству А и не принадлежат множеству В.
Разность множеств А и В обозначают А \ В. Таким образом, по определению разности А \ В = { х | х ∈ А и х ∉В}.
Например, если А = { a , c , k , m , n } и В = { a , b , c , d , e }, то А \ В = { k , m , n }.
Если изобразить А и В при помощи кругов Эйлера-Венна, то разность данных множеств является заштрихованная область (рис. 5).
Определение. Пусть В является подмножеством множества А. В этом случае разность множеств А и В называют дополнением подмножества В до множества А и обозначают В'А. Дополнение можно изобразить как показано на рис. 5. Если В – подмножество универсального множества U, то дополнение подмножества В до U обозначают В'.

Например, если В – множество однозначных натуральных чисел, то В'– множество неоднозначных натуральных чисел, если С – множество равнобедренных треугольников, то С' – множество треугольников, у которых все стороны имеют разную длину.
Разность множеств и дополнение к подмножеству обладают рядом свойств.
1) (А \ В) \ С = (А \ С) \ В.
2) (А∪В) \ С = (А \ С) ∪ (В \ С).
3) (А \ В) ∩ С = (А ∩С) \ (В ∩ С).
4) (А ∪ В)' = А' ∩ В'.
5) (А ∩ В)' = А' ∪В'.
Четвертое свойство формулируется так: дополнение к объединению двух множеств равно пересечению дополнений к этим множествам. Пятое свойство формулируется аналогично.
П р и м е р 1. А – множество натуральных чисел, кратных 3, В – множество натуральных чисел, кратных 5. Задать описанием характеристического свойства множество А \ В и назвать три числа, принадлежащих этому множеству.
Р е ш е н и е. По определению разность данных множеств состоит из натуральных чисел, кратных 3 и не кратных 5. Поэтому разности множеств А и В принадлежат числа 9, 24, 33.
Задания для самостоятельной работы по теме :
Приведите примеры множеств А, В, С, если отношения между ними таковы:

2. Образуйте все подмножества множества букв в слове «крот». Сколько подмножеств получилось?
3. Даны множества А = { a , b , c , d , e , f , k } и В = { a , c , e , k , m , p }. Найдите А ∪ В , А ∩ В , А \ В , В \ А .
4. Из множества N выделили два подмножества: А – подмножество натуральных чисел, кратных 3, и В – подмножество натуральных чисел, кратных 5. Постройте круги Эйлера для множеств N , A , B ; установите, на сколько попарно непересекающихся множеств произошло разбиение множества N ; укажите характеристические свойства этих множеств.
5. Имеется множество блоков, различающихся по цвету (красные, желтые, зеленые), форме (круглые, треугольные, прямоугольные), размеру (большие, маленькие). На сколько классов разбивается множество, если в нем выделены подмножества: А – круглые блоки, В – зеленые блоки, С – маленькие блоки? Сделайте диаграмму Эйлера и охарактеризуйте каждый класс.
6. Известно, что А – множество спортсменов класса, В – множество отличников класса. Сформулируйте условия, при которых: а) А ∩В=Ø б)А U В=А
7. Пусть Х= { x ![]() N/ 1
N/ 1 ![]() x
x ![]() 15}. Задайте с помощью перечисления следующие его подмножества:
15}. Задайте с помощью перечисления следующие его подмножества:
А – подмножество всех четных чисел;
В – подмножество всех нечетных чисел;
С – подмножество всех чисел, кратных 3;
D – подмножество всех чисел, являющихся квадратами;
E – подмножество всех простых чисел.
В каких отношениях они находятся?
6. Рефлексия
Мне больше всего удалось…
Для меня было открытием то, что …
За что ты можешь себя похвалить?
Что на ваш взгляд не удалось? Почему? Что учесть на будущее?
Мои достижения на уроке.
Домашнее задание
ЗАДАЧа № 1.
«В пятых классах школы училось 70 человек. Им было предложено записаться в 3 кружка: по математике, литературе и истории. Староста подсчитал число учащихся, желающих участвовать во внеклассной работе, и получил такие результаты. В кружок по математике записалось 51 человек, по литературе - 40, по истории - 22. 6 человек решили заниматься во всех кружках, математикой и литературой решили заниматься 32 человека, одновременно заниматься математикой и историей решили 11 человек, а литера турой и историей 8 человек. Получив результаты, староста сказал: «Можно подумать, что у нас в 5-х классах обучается не 70 человек, а 170. Все хотят заниматься в кружках».
Однако один из любителей математики сказал: «Что ты, у нас есть ученики, которые не любят ни математику, ни литературу, ни исто рию. Я даже могу сказать, сколько их». Как он узнал?»
ЗАДАЧа № 2.
«В классе 40 человек. Играют в баскетбол 26 человек, занимаются плаванием - 25, ходят на лыжах - 27. Одновременно занимаются плаванием и баскетболом - 15, баскетболом и лыжами - 16, пла ванием и лыжами - 18. Один человек освобожден от занятий по физ культуре. Сколько человек занимается всеми указанными видами спорта? Сколько человек занимается только в одной спортивной секции?».
Задача № 3
Из 40 учащихся класса выписывают газету, 21 – журнал, 15 учащихся – и газету и журнал. Сколько учащихся не выписывают ни журнала, ни газеты?
Задача №4
В классе 35 учеников. 20 человек посещают математический кружок, 11 – биологический. 10 человек не посещают кружков. Сколько биологов увлекается математикой?
ЗАДАЧА №5.
Из 100 человек 85 знают английский язык, 80 – испанский, 75 – немецкий. Все владеют по крайней мере одним иностранным языком. Среди них нет таких, которые знают только два иностранных языка, но есть владеющие тремя языками. Сколько человек знают три иностранных языка?
Методические рекомендации по решению текстовых задач на движение.
Во всех задачах на движение допускается определённая идеализация: считается, что тела движутся прямолинейно и равномерно, скорости (в том числе скорость течения) постоянны в течение определённых промежутков времени, не меняются при поворотах и т.д., движущиеся тела считаются (если не оговорено противное) материальными точками, т.е. не имеющими размеров и массы (вернее, их размеры и масса несущественны для решения задачи). Даже решение задач на движение по окружности не требует применения специальных понятий—угловой скорости и т.п.; здесь точнее было бы говорить о движении по замкнутой трассе.
При решении задач на движение двух тел часто очень удобно считать одно тело неподвижным, а другое—приближающимся к нему со скоростью, равной сумме скоростей этих тел (при движении навстречу) или разности скоростей (при движении вдогонку). Такая базовая модель помогает разобраться с условием задачи и получить нужные уравнения даже в таком относительно трудном случае, как движение по окружности.
Если расстояние между пунктами, из которых начинают движение два тела, не задано, иногда бывает удобно положить его равным единице. Основными типами задач на движение являются следующие:
• задачи на движение по прямой (навстречу и вдогонку),
• задачи на движение по замкнутой трассе,
• задачи на движение протяжённых тел,
• задачи на движение по воде,
• задачи на среднюю скорость.
Рассмотрим более подробно каждый из этих типов задач, выделив, где необходимо, базовые задачи.
Если расстояние между двумя движущимися навстречу друг другу телами равно s, а их скорости— v1 и v2, то время t, через которое они встретятся, находится по формуле t= s / v1+v2. Действительно, если одно из тел считать неподвижным, тогда второе будет приближаться к нему со скоростью, равной сумме скоростей, и пройдёт при этом расстояние, равное расстоянию между телами в момент начала движения, за время, равное отношению этого расстояния к скорости.
Пример 1. Расстояние между городами A и B равно 620 км. Из города A в город B со скоростью 85 км/ч выехал первый автомобиль, а через два часа после этого навстречу ему из города B выехал со скоростью 65 км/ч второй автомобиль. На каком расстоянии от города A автомобили встретятся?
Решение: Через два часа после выезда первого автомобиля расстояние между автомобилями стало равно 620−170=450 (км), поэтому автомобили встретятся через время t = 450/ 85+65 =3 (ч). Таким образом, до момента встречи первый автомобиль будет находиться в пути 5 часов и проедет 85·5=425 км.
Ответ: 425 км.
Если расстояние между двумя телами равно s и они движутся по прямой в одну сторону со скоростями v1 и v2 соответственно (v1 > v2) так, что первое тело следует за вторым, то время t, через которое первое тело догонит второе, находится по формуле t= s / v1+v2 . Действительно, если второе тело считать неподвижным, тогда первое будет приближаться к нему со скоростью, равной разности скоростей, и пройдёт при этом расстояние, равное расстоянию между телами в момент начала движения, за время, равное отношению этого расстояния к скорости.
Пример2. Два пешехода отправляются одновременно из одного и того же места на прогулку по аллее парка. Скорость первого на 1,3 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 520 метрам?
Решение: Время t в часах, за которое расстояние между пешеходами станет равным 520 метрам, т.е. 0,52 (км), находим по формуле t = 0,52 /1,3 =0,4 (ч). Следовательно, это время составляет 24 минуты.
Ответ: 24 минуты.
Рассмотрим теперь движение двух точек по окружности (замкнутой трассе) длины s в одном направлении при одновременном старте из одной точки со скоростями v1 и v2 (v1 > v2) и ответим на вопрос: через какое время первая точка будет опережать вторую ровно на один круг? Считая, что вторая точка покоится, а первая приближается к ней со скоростью v1 - v2, получим, что условие задачи будет выполнено, когда первая точка в первый раз поравняется со второй. При этом первая точка пройдёт расстояние, равное длине трассы, и искомая формула ничем не отличается от формулы, полученной для задачи на движение вдогонку: t= s / v1+v2. Итак, если две точки одновременно начинают движение по окружности (замкнутой трассе) из одной точки в одну сторону со скоростями v1 и v2) соответственно (v1 > v2), то первая точка приближается ко второй со скоростью v1−v2 и в момент, когда первая точка в первый раз догоняет вторую, она проходит расстояние, ровно на один круг большее, чем вторая.
Пример 3. Из одной точки круговой трассы, длина которой равна 12 км, одновременно в одном направлении стартовали два автомобилиста. Скорость первого автомобилиста равна 80 км/ч, и через 48 минут после старта он опережал второго автомобилиста на один круг. Найдите скорость второго автомобилиста.
Решение: Пусть скорость второго автомобилиста равна x км/ч. Поскольку 48 минут составляют 4/5 часа и это и есть то время, за которое первый автомобилист будет опережать второго на один круг, составим по условию задачи уравнение: 12 / 80-x = 4/5
, откуда 320−4x =60, и x =65.
Ответ: 65 км/ч.
В задачах на движение по воде скорость течения считается неизменной. При движении по течению скорость течения прибавляется к скорости плывущего тела, а при движении против течения вычитается из скорости тела. Скорость плота считается равной скорости течения.
Пример 4. Рыболов отправляется на лодке от пристани с намерением вернуться через 7 ч. Перед возвращением он хочет пробыть на берегу 4 ч. На какое наибольшее расстояние он может отплыть, если скорость течения реки равна 1 км/ч, а собственная скорость лодки равна 6 км/ч?
Решение: Пусть искомое расстояние равно x км. Скорость лодки при движении против течения равна 5 км/ч, а при движении по течению равна 7 км/ч. Время, за которое лодка доплывёт от места отправления до места назначения и обратно, равно x /5 + x/ 7 ч. Из условия задачи следует, что это время равно 3 ч. Составим уравнение по условию задачи: x /5 + x/ 7 = 3.
Решив уравнение, получим x =8,75. Ответ: 8,75 км.
Пример 5. Теплоход, скорость которого в неподвижной воде равна 26 км/ч, проходит по течению реки и после стоянки возвращается в исходный пункт. Скорость течения равна 3 км/ч, стоянка длится 8 часов, а в исходный пункт теплоход возвращается через 34 ч после отплытия из него. Сколько километров прошёл теплоход за весь рейс?
Решение: Пусть искомая величина равна 2x. Составим по условию задачи уравнение: x/23 + x/29+8=34,
откуда x/23 + x/29=26.
Далее, (23x+ 29x) / 23*29 =26,
откуда 52x =23·29·26, и 2x =23·29=667.
Ответ: 667 км.
В задачах на движение протяжённых тел требуется, как правило, определить длину одного из них. Наиболее типичная ситуация— определение длины поезда, проезжающего мимо столба или протяжённой платформы. В первом случае поезд проходит мимо столба расстояние, равное длине поезда, во втором случае—расстояние, равное сумме длин поезда и платформы.
Пример 6. По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 120 метров, второй— длиной 80 метров. Второй сухогруз сначала отстаёт от первого на 900 метров, но уже через 27 минут опережает первый на 1,6 километра. На сколько километров в час скорость первого сухогруза меньше скорости второго?
Решение: Будем считать, что первый сухогруз неподвижен, а второй приближается к нему со скоростью x м/мин, равной разности скоростей второго и первого сухогрузов. Тогда за 27 минут второй сухогруз проходит расстояние l= 900 + 80 + 120 + 1600 = 2700 (м). Поэтому x = 2700 /27 =100 м/мин, т.е. 6 км/ч.
Ответ: 6 км/ч.
Напомним, что средняя скорость вычисляется по формуле V = S/ t, где S —путь, пройденный телом, а t —время, за которое этот путь пройден. Если путь состоит из нескольких участков, то следует вычислить всю длину пути и всё время движения. Например, если путь состоял из двух участков протяжённостью s1 и s2,скорости на которых были равны соответственно v1 и v2, то S= s1 + s2, t =t1 +t2, где t1 = S1/ V1 , t2 = S2/ V2.
Пример 7. Первую треть трассы велосипедист ехал со скоростью 18 км/ч, вторую треть—со скоростью 12 км/ч, а последнюю треть— со скоростью 9 км/ч. Найдите среднюю скорость велосипедиста на протяжении всего пути.
Решение. Обозначим длину всей трассы через 3s км. Тогда первую треть трассы велосипедист проехал за время t1 = s /18 , вторую треть— за время t2 = s/12 , последнюю треть—за время t3 = s /9 . Значит, время, потраченное им на весь путь, равно t1 +t2 +t3,
т.е. s/18 +s/12 + s/9 = 45s/ 180 = s/4
Поэтому искомая средняя скорость находится по формуле
V = 3s/ (s/4) = 3s* (4/s) = 12(км/ч). Ответ: 12 км/ч.
ДИДАКТИЧЕСКИЙ МАТЕРИАЛ ДЛЯ УЧАЩИХСЯ
ПО ТЕМЕ «ЗАДАЧИ НА ДВИЖЕНИЕ»
1. Два пешехода выходят навстречу друг другу из разных пунктов, расстояние между которыми 40 км. Если первый выйдет на час раньше второго, то они встретятся через 3 часа после выхода первого. Если второй выйдет на час раньше первого, то они встретятся через 2 часа после выхода первого. С какой скоростью идет каждый пешеход?
2. Два велосипедиста выезжают навстречу друг другу из двух пунктов, расстояние между которыми 50 км. Если первый выедет на час раньше второго, то они встретятся через 2 часа после выезда второго. Если второй выедет на 2 часа раньше первого, то они встретятся через час после выезда первого. С какой скоростью едет каждый велосипедист?
3. Два пешехода выходят навстречу друг другу из двух пунктов, расстояние между которыми 50 км. Если первый выйдет на 3 часа раньше второго, то они встретятся через 4 часа после выхода второго. Скорость первого пешехода на 1 км/ч больше скорости второго. С какой скоростью идет каждый пешеход?
4. Два бегуна выбегают навстречу друг другу из двух пунктов, расстояние между которыми равно 45 км. Сумма скорости бегунов равна 16,5 км/ч. Если первый бегун выбежит на полчаса раньше второго, то они встретятся через 2,5 часа после того, как выбежит второй бегун. С какой скоростью бежит каждый бегун?
5. Два велосипедиста выезжают навстречу друг другу из двух пунктов, расстояние между которыми 80 км. Скорость первого на 3 км/ч меньше скорости второго. Если второй выедет на 1 час раньше первого, то они встретятся через 2 часа после выезда первого. С какой скоростью едет каждый велосипедист?
6. Два пешехода выходят навстречу друг другу из двух пунктов, расстояние между которыми 30 км. Если первый выйдет на 2 часа раньше второго, то он встретит второго пешехода через 4,5 часа после своего выхода. Если второй выйдет на 2 часа раньше первого, то он встретит первого пешехода через 5 часов после своего выхода. С какой скоростью идет каждый пешеход?
![]() Решение: пусть первый пешеход двигался со скоростью х км/ч, а второй со скоростью у км/ч. В первом случае один пешеход пройдет (4,5 х) км, а другой – (2,5 у) км. Во втором случае первый пешеход пройдет (3 х) км, а второй – (5 у) км. Зная, что расстояние между двумя пунктами равно 30 км, можем составить систему уравнений:
Решение: пусть первый пешеход двигался со скоростью х км/ч, а второй со скоростью у км/ч. В первом случае один пешеход пройдет (4,5 х) км, а другой – (2,5 у) км. Во втором случае первый пешеход пройдет (3 х) км, а второй – (5 у) км. Зная, что расстояние между двумя пунктами равно 30 км, можем составить систему уравнений:
![]()
![]()
![]()
![]() 4,5x + 2,5y= 30 9х +5у = 60 6х = 30 х= 5 х=5
4,5x + 2,5y= 30 9х +5у = 60 6х = 30 х= 5 х=5
3х+ 5у = 30 3х + 5 у =30 5у= 30-3х 5у = 15 у =3
Ответ: скорость первого пешехода 5 км/ч, а второго 3 км/ч.
7. Турист, находящийся в спортивном лагере, должен успеть к поезду на железнодорожную станцию. Если он поедет на велосипеде со скоростью 15 км/ч, то опоздает на 30 минут. Если же он поедет на автобусе, скорость которого 40 км/ч, то приедет за 2 часа раньше до отхода поезда. Чему равно расстояние от лагеря до станции?
Решение: пусть расстояние от лагеря до станции равно (х) км. Тогда на велосипеде турист проедет это расстояние за х/15 ч, а на х/40ч. Зная, что в первом случае турист опоздает на 0,5 ч, а во втором приедет на 2 часа раньше срока, составим уравнение:
х/15 – ½ = х/40 +2
8х – 60 = 3 х+ 240
8х-3х =300
х= 60
Ответ: расстояние от лагеря до станции равно 60 км.
8. Николай и Владимир живут в одном доме. Николай вышел из дома и направился к школе. Через 4 минуты после него из дома вышел Владимир и догнал своего друга у школы. Найдите расстояние от дома до школы, если Николай шел со скоростью 60 м/мин, а скорость Владимира 80 м/минуту.
9. Из пункта А в пункт В, расстояние между которыми равно 8 км, одновременно вышли два лыжника. Скорость одного из них на 4 км/ч меньше скорости другого. Лыжник, который первым прибыл в пункт В, сразу же повернул обратно и встретил другого лыжника через 45 мин. после выхода из пункта А. На каком расстоянии от пункта В произошла встреча?
10. Из пункта А в пункт В, расстояние между которыми 25 км, одновременно выехали автобус и автомобиль. Во время пути автомобиль сделал остановку на 2 мин., но в пункт В приехал на 3 мин. раньше автобуса. Найдите скорости автомобиля и автобуса, если известно, что скорость автобуса в 1,2 раза меньше скорости автомобиля.
Решение: пусть скорость автобуса (х) км/ч, тогда скорость автомобиля (1,2 х) км/ч. Таким образом, время движения автобуса (25/x) ч, а автомобиля
(25/ 1,2х) ч. Зная, что автомобиль сделал остановку на 2 мин., но приехал на 3 мин. раньше автобуса, составим уравнение:
25/х – (25/1,2х + 1/30) = 1/20,
2 мин = 1/30 ч., 3 мин. = 1/20 ч.
ОДХ: х не равно нулю.
25/х – 25/1,2х - 1/30 = 1/20,
25/х – 25/1,2х = 5/ 60,
( 25*1,2 - 25) / 1,2х = 5/ 60
( 30-25 ) / 1,2х = 5/ 60
1,2х*5 = 5* 60
6х = 300
х= 50
1. ![]() 1,2 = 60 (км/ч) – скорость автомобиля.
1,2 = 60 (км/ч) – скорость автомобиля.
Ответ: 50 км/ч – скорость автобуса; 60 км/ч – скорость автомобиля.
11. Катер, собственная скорость которого 8 км/ч, прошел по реке расстояние, равное 15 км, по течению и такое же расстояние против течения реки. Найдите скорость течения реки, если время, затраченное на весь путь, равно 4 часа.
Решение: пусть скорость течения реки равна (х) км/ч, тогда (8-х) км/ч – скорость катера против течения реки, а (8+х) км/ч – скорость катера по течению реки. Запишем и решим уравнение:
15* (8-х) + 15* (8+х) = 4(8+х)*(8-х)
120 – 15х +120+15х = 4* (8-х)*(8+х)
240=256- 4х²
4х² = 16
х²=4
х=2
х= -2
т.к. х = -2 не подходит по смыслу задачи, то х=2.
Ответ: 2 км/ч – скорость течения реки.
12. Моторная лодка отправилась по реке от одной пристани к другой и через 2,5 часа вернулась обратно, затратив на стоянку 25 минут. Найдите скорость течения реки, если собственная скорость лодки равна 20 км/ч, а расстояние между пристанями 20 км.
13. За 7 часов катер прошел 60 км по течению реки и 64 км против течения. В другой раз катер за 7 часов прошел 80 км по течению реки и 48 км против течения. Определите собственную скорость катера и скорость течения реки.
14. Катер проплывает 8 км против течения реки и еще 30 км по течению за то же время, за которое плот может проплыть по этой реке 4 км. Скорость катера в стоячей воде равна 18 км/ч. Найдите скорость плота.
15. На соревнованиях по кольцевой трассе один лыжник проходил круг на 2 мин. быстрее другого и через час обогнал его ровно на круг. За сколько минут каждый лыжник проходил круг?
16. На соревнованиях по картингу по кольцевой трассе один из картов проходил круг на 5 мин. медленнее другого и через час отстал от него ровно на круг. За сколько минут каждый карт проходил круг?
Решение: пусть первый карт проходит круг за (х) мин., тогда второй карт проходит круг за (х+5) мин. Составим и решим уравнение:
60/х – 60/ х+5 = 1*(х+5), ОДЗ: х не равно 0 и - 5
60(х+5) – 60х = х² + 5х
60х + 300 - 60х= х²+ 5х
х² + 5х - 300 = 0
х1= 15, х2 = -20
Т.к. по смыслу задачи ![]()
![]() 0, то х=15
0, то х=15
1. 15 + 5 = 10 (мин.) время движения второго карта.
Ответ: за 15 минут первый карт проходит круг, за 20 мин. второй карт проходит круг.
17. По окружности длиной 60 м равномерно в одном направлении движутся две точки. Одна из них совершает полный оборот на 5 с быстрее другой. При этом совпадение точек происходит каждый раз через 1 минуту. Определите скорости движения точек.
18. Дорога от поселка до станции идет сначала в гору, а потом под гору, при этом ее длина равна 9 км. Пешеход на подъеме идет со скоростью, на 3 км/час меньшей, чем на спуске. Путь от поселка до станции занимает у него 2 часа, а обратный путь – 2 ч. 30 мин. Определите длину подъема на пути к станции и скорость пешехода на подъеме и на спуске.
Методические рекомендации по решению текстовых задач на производительность и работу, проценты и концентрацию
В определённом смысле задачи на производительность (работу) схожи с задачами на движение: роль скорости здесь играет производительность, роль расстояния—объём работы. В тех случаях, когда объём работы в явном виде не задан, его иногда удобно принять равным единице. Существенно разных задач здесь практически нет, во всех случаях речь идёт о выполнении определённой работы, меняются только сюжеты, а «математическая» фабула остаётся одной и той же. Иногда в задачах на работу выделяют группу задач на трубы и бассейны, решение которых, вообще говоря, не имеет никаких специфических черт по сравнению с другими задачами на работу.
В некоторых случаях при решении задач на совместную работу можно обойтись без решения уравнений, используя только арифметический способ. Правда, для этого порой приходится прибегать к гипотетическим допущениям.
Пример 1. Маша и Даша за день пропалывают 3 грядки, Даша и Глаша— 4 грядки, а Глаша и Маша— 5 грядок. Сколько грядок за день смогут прополоть девочки, работая втроём?
Решение: Вообразим, что сначала Маша и Даша работали один день, затем Даша и Глаша работали один день, а потом Глаша и Маша работали ещё один день. Получается, что каждая из девочек работала два дня, или что бригада, состоящая из Маши, Глаши и Даши, прополола 3+4+5=12 грядок за два дня. Значит, за один день эта бригада прополет вдвое меньше грядок, т.е. 6.
Ответ: 6.
Ключевой в задачах на работу является следующая.
Пример 2. Первый мастер может выполнить некоторую работу за a часов, а второй мастер—за b часов. За какое время выполнят работу оба мастера, работая вдвоём?
Решение: Поскольку объём работы не задан, его можно принять равным единице. Тогда первый мастер за один час выполнит часть работы, равную 1 /a , второй— 1/ b , а оба мастера— 1/ a + 1 /b . Значит, всю работу они выполнят за время t= 1/ (1/a + 1/b) ч.
Ответ: t= 1/ (1/a + 1/b) ч.
Пример 3. Каждый из двух рабочих одинаковой квалификации может выполнить заказ за 12 часов. Через 3 часа после того, как один из них приступил к выполнению заказа, к нему присоединился второй рабочий, и работу над заказом они довели до конца уже вместе. Сколько часов потребовалось на выполнение всего заказа?
Решение: Вдвоём рабочие за час делают 2 /12 = 1/ 6 всей работы. За 3 часа первый рабочий сделал 3 /12 = 1/ 4 всей работы. Оставшиеся 3 /4 работы рабочие делали уже вместе и потратили на это 3/ 4 : 1/ 6 = 4,5 ч. Значит, время, затраченное на выполнение всего заказа, составляет 7,5 часов.
Ответ: 7,5 ч.
Как уже отмечалось, в задачах на бассейны и трубы нет ничего специфического по сравнению с другими задачами на совместную работу. Модельная ситуация остаётся той же, только мастерам будут соответствовать трубы или насосы разной производительности, а работа будет заключаться в наполнении бассейна или иного резервуара.
Пример 4. Первая труба пропускает на 6 литров воды в минуту меньше, чем вторая труба. Сколько литров воды в минуту пропускает первая труба, если бак объёмом 360 литров она заполняет на 16 минут медленнее, чем вторая труба?
Решение: Пусть первая труба пропускает x литров воды в минуту, x >0. Тогда вторая труба пропускает x +6 литров воды в минуту. Составим по условию задачи уравнение: 360 /x = 360/( x +6) +16. Разделив обе части уравнения на 8, получим 45/ x = 45/( x +6) +2, и, следовательно, 45/ x – 45/( x +6) =2. Приведём дроби в левой части к общему знаменателю: 45(x +6)−45x/ x(x +6) =2, откуда 2x(x +6)=45·6,и,значит, x2 +6x−135=0. Корнями полученного квадратного уравнения являются числа −15 и 9, из которых только последнее удовлетворяет условию x >0.
Ответ: 9 л.
ДИДАКТИЧЕСКИЙ МАТЕРИАЛ ДЛЯ УЧАЩИХСЯ
ПО ТЕМЕ «ЗАДАЧИ НА СОВМЕСТНУЮ РАБОТУ»
1. Две трубы при совместной работе могут наполнить бассейн за 4 часа. Если бы сначала первая труба наполнила половину бассейна, а затем ее перекрыли и открыли вторую, то наполнение бассейна было бы закончено за 9 часов. За сколько часов может наполнить этот бассейн каждая труба в отдельности?
Решение: вся работа равна 1. Пусть первая труба заполнит бассейн за (х) час., а вторая – за (у) час. Составим и решим систему уравнений:
4/х+4/у=1 4у +4х=ху 4(18-х) + 4х = 4(18-х)
х/2 + у/2=9 х+у = 18 у= 18-х
х²-18х+72= 0 х1 = 12 х2 = 6
у= 18-х у1 = 6 у1= 12
Ответ одна труба может заполнить бассейн за 12 час., а вторая – за 6 час.
2. Одна из труб может наполнить водой бак на 10 мин. быстрее другой. За какое время может наполнить этот бак каждая труба, если при совместном действии этих труб в течение 8 мин. было заполнено 2/3 бака?
Решение: пусть одна труба заполняет бак за (х) мин., тогда вторая труба заполнит бак за (х + 10) мин. Составим и решим уравнение:
8/х + 8/ (х+10) =2/3
24 (х+10) + 24х = 2х(х+10)
2х² - 28х - 240 = 0
х1 = 20
х2= -6 – не подходит по смыслу задачи
1) 20 + 10 = 30 мин.
Ответ: первая труба заполнит бак за 20 мин., а вторая – за 30 мин.
3. В бассейн проведены две трубы разного сечения. Одна равномерно подает, а вторая равномерно отводит воду, причем через первую бассейн наполняется на 2 часа дольше, чем через вторую опорожняется. При заполненном на 1/3 бассейна были открыты две трубы, и бассейн оказался пустым спустя 8 час. За сколько часов, действуя отдельно, первая труба наполняет, а вторая опорожняет бассейн.
4. Четыре бригады должны разгрузить вагон с продуктами. Вторая, третья и четвертая бригады вместе могут выполнить эту работу за 4 ч.; первая, третья и четвертая – за 3 часа. Если же будут работать только первая и вторая бригада, то вагон будет загружен за 6 час. За какое время могут разгрузить вагон все четыре бригады, работая вместе?
5. Две бригады, работая вместе, должны отремонтировать участок дороги за 18 дней. В действительности же получилось так, что сначала работала первая бригада, а заканчивала ремонт участка дороги вторая бригада. В результате ремонт участка дороги продолжался 40 дней, причем первая бригада в свое рабочее время выполнила 2/3 всей работы. За сколько дней был бы отремонтирован участок дороги каждой бригадой отдельно?
6. Одна мельница может смолоть 38 ц пшеницы за 6 часов, другая - 96 ц за 15 часов, третья – 35 ц за 7 часов. Как распределить 133 т пшеницы между мельницами, чтобы они мололи зерно в течение одного и того же времени.
7. Лесхоз планировал заготовить за несколько дней 216 новогодних елей. Первые три дня лесхоз выполнял установленную ежедневную норму, а потом стал заготавливать на 2 ели в день больше. Поэтому уже за 1 день до срока было заготовлено 232 ели. Сколько елей ежедневно заготавливал лесхоз в первые три дня работы.
8. Машинистка должна была напечатать за определенное время 200 страниц. Печатая в день на 5 страниц больше, чем планировала, она завершила работу на два дня раньше срока. Сколько страниц в день печатала машинистка?
Решение: пусть машинистка фактически набирала (х) страниц в день, тогда по плану она должна была набирать (х - 5) страниц в день. Таким образом планировалось напечатать 200 страниц за 200 : (х-5) дней, в то время как машинистка справилась с работой на 2 дня раньше. Составим и решим уравнение:
200/ (х-5) – 200/ х = 2 ОДЗ: х не равно 0 и 5
200х – 200(х-5) = 2х(х-5)
х²-10х-1000 =0
х1 = 25,
х2=-20 – не подходит по смыслу задачи
Ответ: машинистка печатала по 25 страниц в день.
9. Николай планировал, что сможет хорошо подготовиться к экзамену, если будет решать по 12 задач в день. Однако ежедневно он перевыполнял свою норму на 8 задач и уже за 5 дней до экзамена решил на 20 задач больше, чем планировал сначала. Сколько задач решил Коля?

Новости
Онлайн-олимпиада по математике для учеников 1–11 классов
Основной тур:16 нояб. – 20 дек. 2020
https://ru.bricsmath.com/teachers/classes